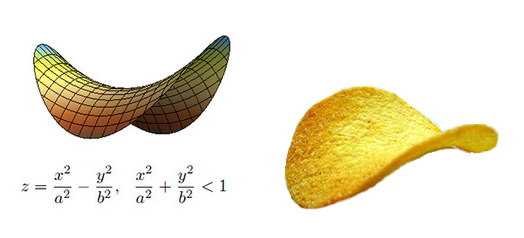Smak matematyki
Do matematyki przez żołądek

Wszyscy wiemy, że z sympatią do matematyki bywa różnie. Ale
jest na to sposób:)
W życiu często, gdy chcemy dotrzeć do serca sympatii i żadne sposoby nie
skutkują, to wykorzystujemy stare polskie przysłowie: „Przez żołądek do serca”.
Zatem zobaczmy jak może „smakować” matematyka.
Oto
moje propozycje na posmakowanie matematyki w nieco inny sposób:
1. Matematyczna
szarlotka – „π”
Szarlotkę większość z
nas lubi. Co do składu ciasta, dodatków, itp. to już
Wam pozostawiam:)

Pizzę też większość lubi, więc proponuję
zrobić ją w swoim ulubionym smaku, ale obowiązkowo dołączyć coś matematycznego,
np. można również wykorzystać liczbę Pi zdobiąc pizzę w taki oto sposób:
Będziemy
potrzebować tradycyjny obwarzanek, jak na zdjęciu

Po
odpowiednim przecięciu otrzymamy coś takiego:

A teraz
posmarujmy czymś dobrym i smacznego!

Nie jest to
trudne do wycięcia, ale jednak najlepiej to zobaczyć, zatem poniżej film, na
którym dowiecie się jak to wykonać.
4. Stek Möbiusa na obiad
Odpowiednio
skręcamy podłużny kawałek dobrego mięska w ten oto sposób:

A po wypieczeniu otrzymujemy:

5. Fraktalne
ciasteczka w postaci
„Dywanu Sierpińskiego”
Dywan Sierpińskiego to słynny fraktal.
Można go wykonać również w postaci jadalnych ciasteczek. Co do składu ciasta,
to tutaj nie ingeruję, a jedynie pokażę jak połączyć fragmenty ciasta, aby
otrzymać takie oto ładne ciasteczka.

Krótka obrazkowa instrukcja „montażu” :

Można w podobny sposób zrobić
ciasteczka przedstawiające fraktal Kocha, czyli popularny płatek śniegu.

6. Fraktalny piernik w kształcie sześcianu
czyli Kostka Mengera
Pomysł z przykładu 4. możemy przenieść na wymiar 3D. Przy tym jest trochę
więcej pracy, ale i efekt robi wrażenie. Aż szkoda zjeść.

Kilka fotek z poszczególnych etapów powstania.

7.
Fraktalny Hamantaszen
Hamantaszen - tradycyjne dla kuchni żydowskiej
nadziewane ciasteczka w kształcie trójkąta. Ale ten będzie nieco bardziej
rozbudowany. Wykorzystamy tu trójkąt Sierpińskiego, a więc mamy kolejną fraktalną
potrawę.

Ciasteczka wypiekane są na święto
Purim, które przypada na przełom lutego i marca. Upamiętnia ono ocalenie Żydów
od rzezi w starożytnej Persji.
Ponieważ ta potrawa to dla nas coś
nowego, to podaję małe wskazówki z Wikipedii:
„Hamantaszen przygotowuje się z mąki,
proszku do pieczenia, oleju, cukru, wanilii lub cynamonu, skórki cytrynowej i
pomarańczowej. Ciasto może też być francuskie lub drożdżowe. Tradycyjny farsz
jest makowy z udziałem miodu i bakalii – rodzynek, fig, daktyli i orzechów.
Współcześnie ciastka nadziewa się także dżemem, powidłami lub innymi masami."
8. Łańcuch z
jabłka – czyli
trochę witamin w oryginalnym kształcie

Spróbujcie z jabłka zrobić coś takiego. Tym razem nie będę
podpowiadał jak to wykonać. Nie jest to łatwe, wykorzystajcie trochę sposób
cięcia obwarzanki z przykładu 3.
9.
Suszone
jabłka, ale w jakim
kształcie!
Każdy z nas może wykonać takie jabłka
bez żadnych problemów. Wystarczy pokroić jabłko na plasterki i zostawić do
wysuszenia. Kształt, który jabłko uzyskuje to często, tzw. paraboloida
hiperboliczna:


10. Hiperboliczne
crunchipsy
Jeżeli nie
uda Wam się uzyskać takich kształtów z jabłka, to zawsze można kupić crunchipsy
w takim kształcie, ale zanim je zjecie przyjrzyjcie się na ten kształt
paraboloidy hiperbolicznej. Jednak do jedzenia polecam te z jabłek.
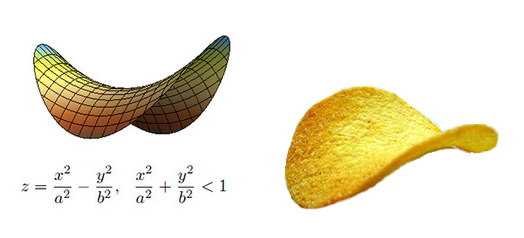
11. Platońskie
jabłka
Bryły platońskie to wielościany foremne, których wszystkie ściany są
wielokątami foremnymi i przystającymi oraz w których z każdego wierzchołka
wychodzi tyle samo krawędzi.

Zatem sami widzicie, że matematyka
może całkiem nieźle smakować, przez co z pewnością ją polubimy.
Smacznego!
Bibliografia:
1.
www.wikipedia.org
2.
www.georgehart.com
3.
www.evilmadscientist.com
4.
www.flickr.com
2014
Tomasz Grębski