Zadanie 1. [Politechnika Warszawska - 2009 FINAŁ]
Znaleźć wszystkie pary $$(x, y)$$ liczb rzeczywistych spełniające układ równań
$$
\left\{\begin{array}{l}
\sqrt{\frac{x}{y}}+\sqrt{\frac{y}{x}}=\frac{7}{\sqrt{x y}}+1 \\
x \sqrt{x y}+y \sqrt{x y}=78
\end{array}\right.
$$
$$\mathrm{Z}$$ pierwszego równania otrzymujemy, że $$x, y$$ muszą być tego samego znaku (i nie mogą być zerami). Jednak gdy rozważymy drugie równanie i przyjmiemy, że $$x, y$$ są ujemne, wtedy lewa strona równania będzie ujemna, a prawa dodatnia sprzeczność.
Stąd wnioskujemy, że $$x, y$$ muszą być liczbami dodatnimi. Pomnóżmy pierwsze równanie przez $$\sqrt{x y}$$ :
$$
\left\{\begin{array}{l}
x+y=7+\sqrt{x y} \\
\sqrt{x y}(x+y)=78
\end{array}\right.
$$
Podstawmy $$u=x+y, v=\sqrt{x y}$$ (oczywiście $$u, v>0$$ ):
$$
\begin{aligned}
& \left\{\begin{array}{l}
u=7+v \\
u v=78
\end{array}\right. \\
& (7+v) v=78 \\
& v^2+7 v-78=0 \\
& (v-6)(v+13)=0 \\
& v=6 \quad \vee \quad v=-13 \\
&
\end{aligned}
$$
Ale $$v>0$$ :
$$
\begin{aligned}
& \left\{\begin{array}{l}
v=6 \\
u=13
\end{array}\right. \\
& \left\{\begin{array}{l}
\sqrt{x y}=6 \\
x+y=13
\end{array}\right. \\
& \left\{\begin{array}{l}
x y=36 \\
y=13-x
\end{array}\right. \\
& x(13-x)=36 \\
& x^2-13 x+36=0 \\
& (x-4)(x-9)=0 \\
&
\end{aligned}
$$
Dla $$x=4$$ mamy $$y=9$$
Dla $$x=9$$ mamy $$y=4$$
Rozwiązaniami są dwie pary: $$(x, y)=(4,9),(x, y)=(9,4)$$.
Zadanie 2. [Politechnika Warszawska - 2009 FINAŁ]
W trójkącie równoramiennym wysokości względem podstawy i ramienia mają długości $$12 \mathrm{~cm}$$ i odpowiednio $$14,4 \mathrm{~cm}$$. Obliczyć stosunek promienia koła wpisanego w ten trójkąt do promienia koła na nim opisanego.
Przyjmijmy oznaczenia jak na rysunku:
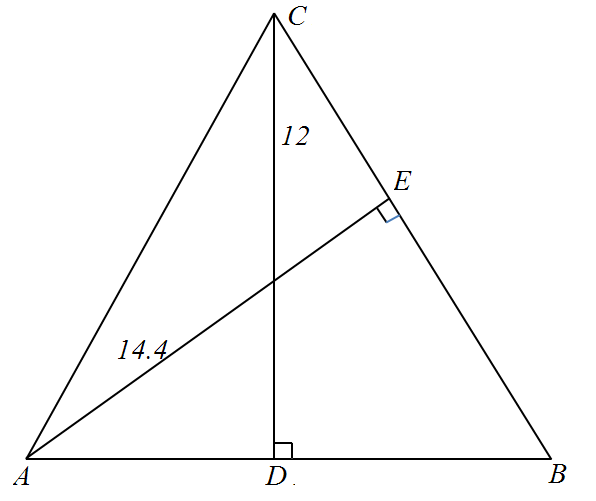
Ponadto niech $$|A B|=a,|B C|=b$$, wtedy $$|D B|=\frac{a}{2}$$. $$\mathrm{Z}$$ tw. Pitagorasa w $$\triangle D B C$$:
$$
\begin{aligned}
& \left(\frac{a}{2}\right)^2+12^2=b^2 \\
& b=\sqrt{144+\frac{a^2}{4}}
\end{aligned}
$$
Ponieważ $$\triangle A B E \sim \triangle C D B(\mathrm{k}-\mathrm{k}-\mathrm{k})$$, to:
$$
\begin{gathered}
\frac{|A E|}{|A B|}=\frac{|C D|}{|C B|} \\
\frac{14.4}{a}=\frac{12}{\sqrt{144+\frac{a^2}{4}}}
\end{gathered}
$$
Stąd otrzymamy $$a=18$$, więc $$b=15$$.
Wtedy:
$$
P_{A B C}=\frac{1}{2} a \cdot 12=108
$$
Korzystając ze wzorów:
$$
P_{A B C}=\frac{(a+b+b) r}{2} \quad P_{A B C}=\frac{a b b}{4 R}
$$
Gdzie $$r, R$$ to odpowiednio długości promieni okręgów wpisanego i opisanego:
$$
\begin{aligned}
& 108=\frac{48 r}{2} \quad 108=\frac{18 \cdot 15 \cdot 15}{4 R} \\
& r=\frac{9}{2} \quad R=\frac{75}{8} \\
&
\end{aligned}
$$
Więc szukany stosunek wynosi:
$$
\frac{r}{R}=\frac{12}{25}
$$
Zadanie 3. [Politechnika Warszawska - 2009 FINAŁ]
W talii złożonej z 52 kart jest po 13 pików, kierów, kar i trefli. W każdym kolorze jest as, król, dama, walet i karty od dziesiątki do dwójki. W grze w pokera fulem nazywamy układ 5 kart składający się z trzech kart tego samego typu oraz pary kart tego samego typu, np.: 3 króle i 2 asy. Wylosowanie dowolnych 5 kart z tej talii jest tak samo prawdopodobne. Jakie jest prawdopodobieńst wo wylosowania fula?
Niech $$\Omega$$ - oznacza wszystkie możliwości wylosowania pięciu kart z talii. Oczywiście:
$$
|\Omega|=\left(\begin{array}{c}
52 \\
5
\end{array}\right)
$$
Niech $$A$$ - oznacza wszystkie możliwości uzyskania fula.
$$
\text { Wtedy }|A|=\left(\begin{array}{c}
13 \\
1
\end{array}\right)\left(\begin{array}{l}
4 \\
3
\end{array}\right)\left(\begin{array}{c}
12 \\
1
\end{array}\right)\left(\begin{array}{l}
4 \\
2
\end{array}\right) \text {. }
$$
Najpierw wybieramy jedną z trzynastu figur (od 2 do asa), następnie z czterech kolorów dobieramy trzy, w ten sposób otrzymamy trzy karty, które utworzą nam część fula. Następnie wybieramy jedną z dwunastu pozostalych figur, a następnie z czterech kolorów dobieramy dwa.
Stąd szukane prawdopodobieństwo jest równe:
$$
P(A)=\frac{|A|}{|\Omega|}=\ldots=\frac{4}{4165}
$$
Zadanie 4. [Politechnika Warszawska - 2009 FINAŁ]
Wykazać, że liczba
$$
3 \cdot 7 \cdot 11 \cdot 29 \cdot 40 \cdot 299 \cdot \sin 10^{\circ} \cdot \cos 160^{\circ} \cdot \sin 130^{\circ} \cdot\left[\frac{1}{2} \log _{\frac{1}{2}}(2+\sqrt{3})+\log _{\frac{1}{2}}(\sqrt{6}-\sqrt{2})\right]
$$
jest liczbą naturalną. Ile dzielników będących liczbami naturalnymi ma ta liczba?
Obliczmy (będziemy korzystać ze wzoru $$\sin \alpha \cos \alpha=\frac{1}{2} \sin 2 \alpha$$ oraz ze wzorów redukcyjnych):
$$
\begin{gathered}
\sin 10^{\circ} \cos 160^{\circ} \sin 130^{\circ}=\sin 10^{\circ} \cos \left(180^{\circ}-160^{\circ}\right) \sin \left(90^{\circ}+40^{\circ}\right)= \\
=-\sin 10^{\circ} \cos 20^{\circ} \cos 40^{\circ}=-\frac{\cos 10^{\circ} \sin 10^{\circ} \cos 20^{\circ} \cos 40^{\circ}}{\cos 10^{\circ}}= \\
=-\frac{\frac{1}{2} \sin 20^{\circ} \cos 20^{\circ} \cos 40^{\circ}}{\cos 10^{\circ}}=-\frac{\frac{1}{4} \sin 40^{\circ} \cos 40^{\circ}}{\cos ^{\circ}}= \\
=-\frac{\frac{1}{8} \sin 80^{\circ}}{\cos 10^{\circ}}=-\frac{\frac{1}{8} \cos 10^{\circ}}{\cos 10^{\circ}}=-\frac{1}{8}
\end{gathered}
$$
Ponadto:
$$
\begin{gathered}
\frac{1}{2} \log _{\frac{1}{2}}(2+\sqrt{3})+\frac{1}{2} \log _{\frac{1}{2}}(\sqrt{6}-\sqrt{2})^2=\frac{1}{2}\left(\log _{\frac{1}{2}}(2+\sqrt{3})+\log _{\frac{1}{2}}(6-2 \sqrt{12}+2)\right)= \\
=\frac{1}{2}\left(\log _{\frac{1}{2}}(2+\sqrt{3})+\log _{\frac{1}{2}}(8-4 \sqrt{3})\right)=\frac{1}{2} \log _{\frac{1}{2}}[(2+\sqrt{3}) 4(2-\sqrt{3})]= \\
=\frac{1}{2} \log _{\frac{1}{2}} 4=\log _{\frac{1}{2}} 2=-1
\end{gathered}
$$
Nasza liczba jest więc równa:
$$
M=3 \cdot 7 \cdot 11 \cdot 29 \cdot 8 \cdot 5 \cdot 13 \cdot 23 \cdot\left(-\frac{1}{8}\right) \cdot(-1)=3 \cdot 7 \cdot 11 \cdot 29 \cdot 5 \cdot 13 \cdot 23
$$
Jako iloczyn liczb naturalnych liczba $$M$$ jest liczbą naturalną.
Liczbę $$M$$ przedstawiliśmy jako iloczyn siedmiu różnych liczb pierwszych.
By utworzyć dzielnik liczby $$M$$ musimy wybrać jakiś podzbiór z tych 7 liczb pierwszych i wymnażając liczby z tego podzbioru utworzyć dzielnik (gdy wybierzemy zbiór pusty, przymijmy, że dzielnikiem jest 1). Stąd ilość dzielników liczby $$M$$ jest równa ilości podzbiór zbioru 7-elementowego, czyli $$2^7=128$$.
Zadanie 5. [Politechnika Warszawska - 2009 FINAŁ]
Dany jest czworościan $$A B C D$$ o krawędziach długości: $$|B C|=a$$, $$|A C|=b,|A B|=c,|A D|=d,|B D|=e,|C D|=f$$. Punkt $$S$$ jest środkiem ciężkości trójkąta $$A B C$$.
Dowieść, że
$$
|D S|=\frac{1}{3} \sqrt{3 d^2+3 e^2+3 f^2-a^2-b^2-c^2}
$$
Przyjmijmy oznaczenia:
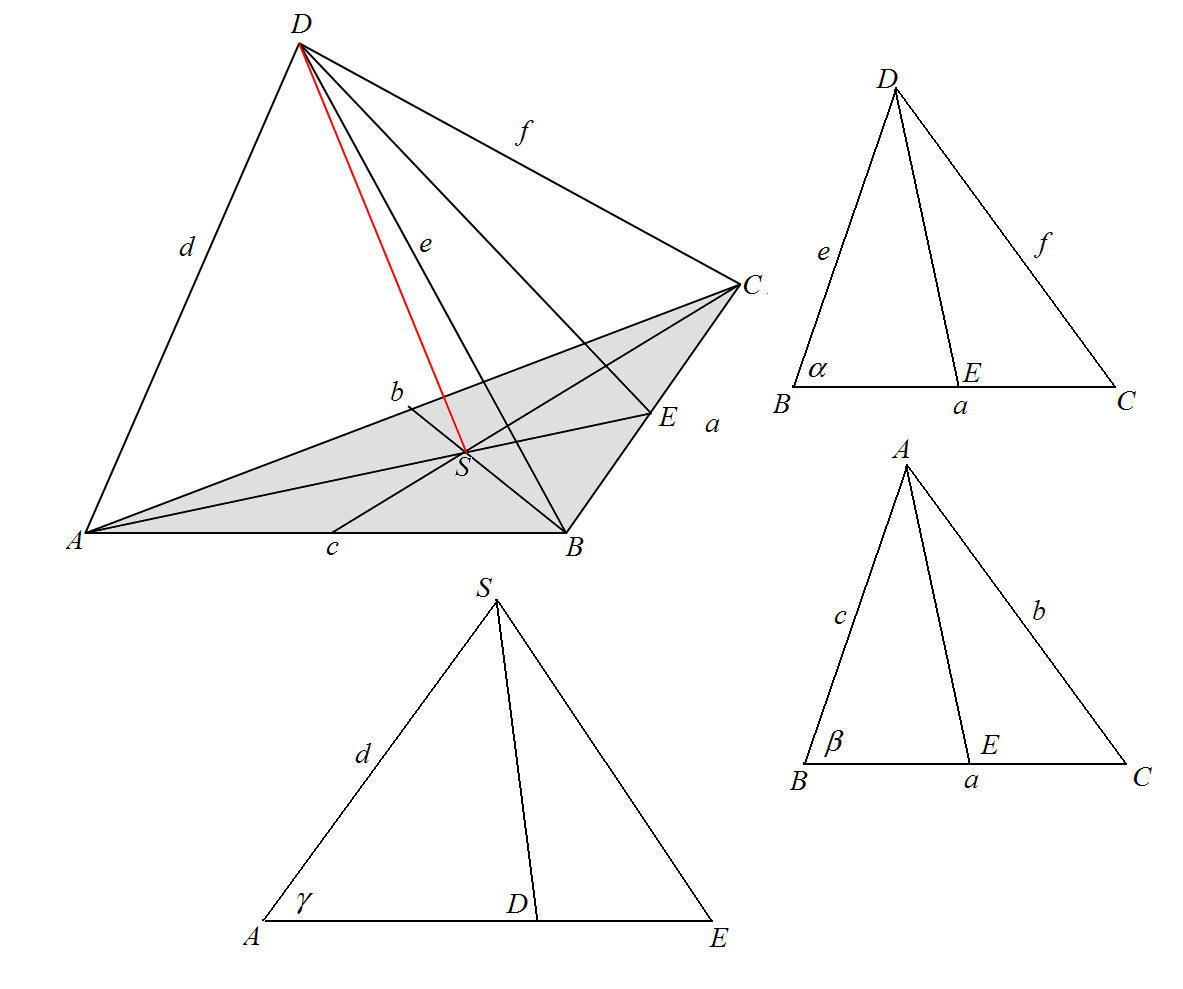
Skoro $$S$$ jest środkiem cięzkości trójkąta $A B C$$, to jest to punkt przecięcia się środkowych w tym trójkącie.
- Popatrzmy na przekrój $$B C D$$, oczywiście $$|B E|=\frac{a}{2}$$. $$\mathrm{Z}$$ tw. cosinusów w trójkątach: $$B C D$$ oraz $$B E D$$ otrzymujemy układ równań:
$$
\left\{\begin{array}{l}
|D E|^2=\frac{a^2}{4}+e^2-2 \cdot \frac{a}{2} \cdot e \cos \alpha \\
f^2=a^2+e^2-2 a e \cos \alpha
\end{array}\right.
$$
Mnożymy pierwsze równanie przez 2:
$$
\left\{\begin{array}{l}
2|D E|^2=\frac{a^2}{2}+2 e^2-2 a e \cos \alpha \\
f^2=a^2+e^2-2 a e \cos \alpha
\end{array}\right.
$$
Odejmujemy stronami:
$$
\begin{aligned}
& 2|D E|^2-f^2=-\frac{a^2}{2}+e^2 \\
& |D E|^2=\frac{2 e^2+2 f^2-a^2}{4}
\end{aligned}
$$
- Popatrzmy na przekrój $$B C A$$, w analogiczny sposób wyznaczamy długość $$|A E|$$ :
$$
|A E|^2=\frac{2 b^2+2 c^2-a^2}{4}
$$
- Popatrzmy na przekrój $$A E D$$. Oczywiście $$|A S|=\frac{2}{3}|A E|$$ (środkowe przecinają się w jednym punkcie, który dzieli je w stosunku $$2: 1$$, licząc od wierzchołka w trójkącie).
Analogicznie jak wcześniej stosujemy tw. cosinusów dla trójkątów $$A S D$$ oraz $$A E D$$ :
$$
\left\{\begin{array}{l}
|D S|^2=d^2+\left(\frac{2}{3}\right)^2|A E|^2-2 d \cdot \frac{2}{3}|A E| \cos \gamma \\
|D E|^2=d^2+|A E|^2-2 d|A E| \cos \gamma
\end{array}\right.
$$
Mnożymy pierwsze równanie przez $$\frac{3}{2}$$ i odejmujemy stronami równania:
$$
\frac{3}{2}|D S|^2-|D E|^2=\frac{1}{2} d^2-\frac{1}{3}|A E|^2
$$
Wykorzystując wcześniej obliczone wielkości $$|D E|^2$$ oraz $$|A E|^2$$ otrzymamy:
$$
\begin{aligned}
& |D S|^2=\frac{1}{9}\left(3 d^2+3 e^2+3 f^2-a^2-b^2-c^2\right) \\
& |D S|=\frac{1}{3} \sqrt{3 d^2+3 e^2+3 f^2-a^2-b^2-c^2}
\end{aligned}
$$

