Matura 2022 - zmiany
Matura Odsłon: 4128

MATURA Z MATEMATYKI 2022 - CO SIĘ ZMIENIŁO?

 

Na zdjęciach wyróżnione zostały zagadnienia (lub części zagadnień), które zostały usunięte z wymagań maturalnych.

 

 

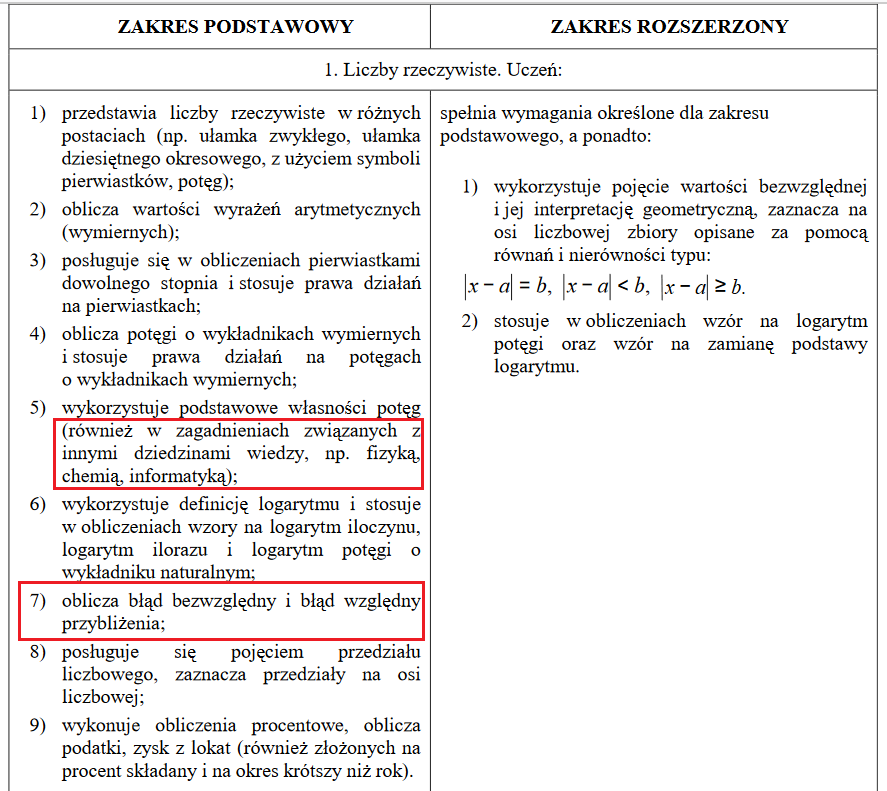
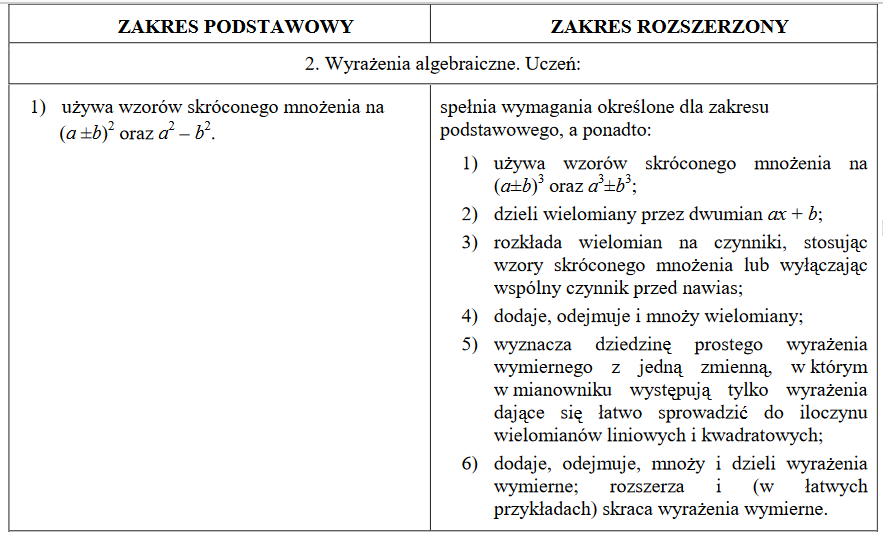
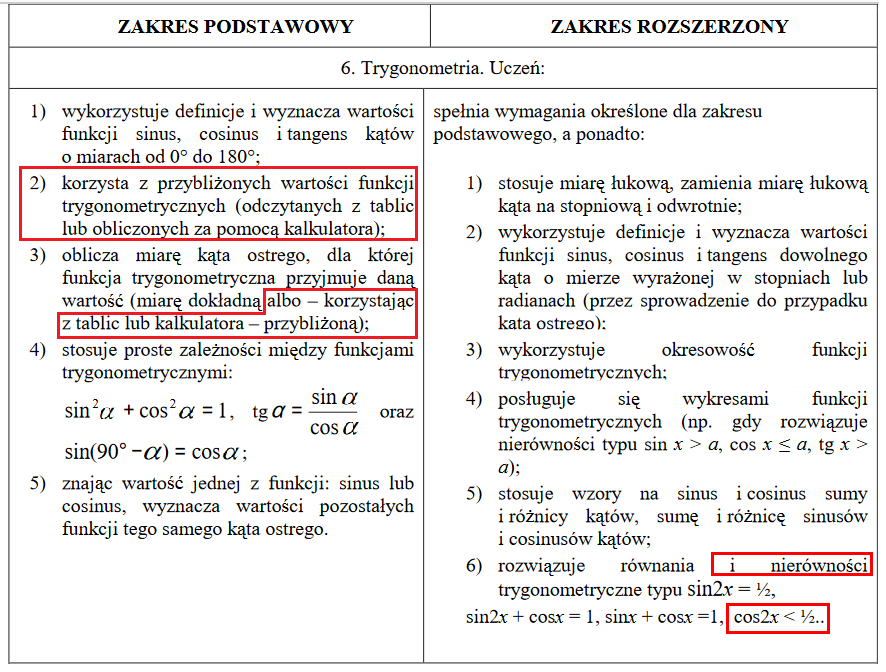
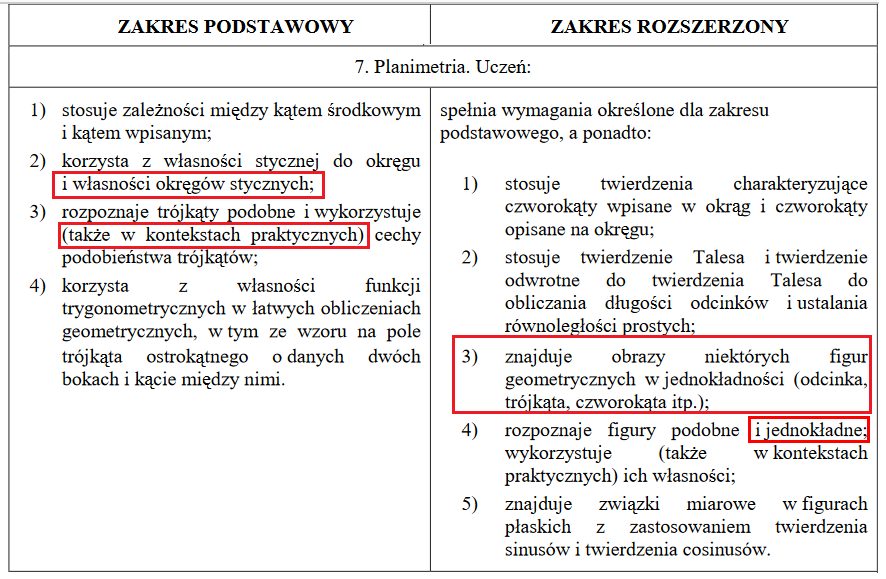
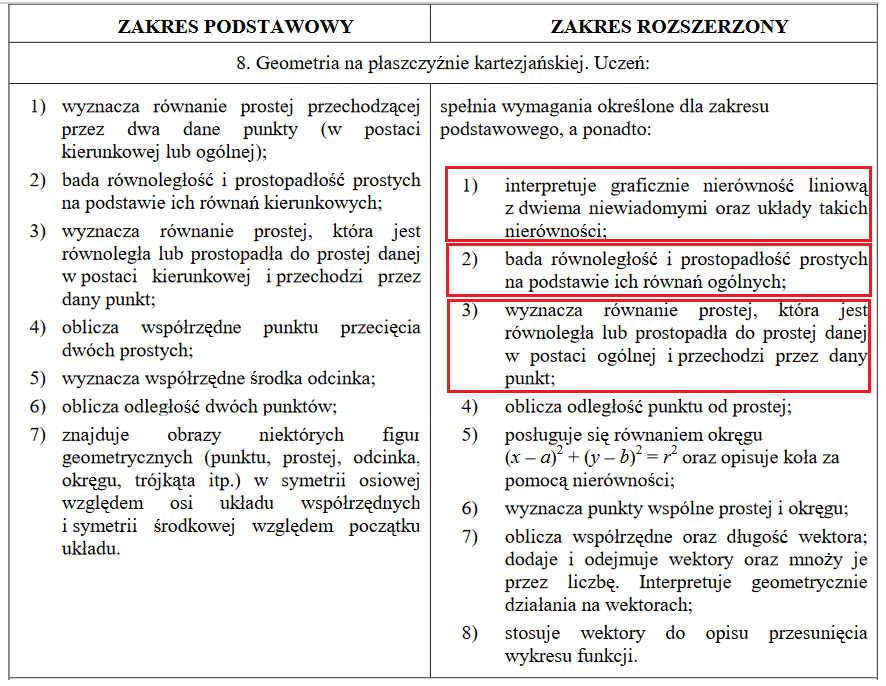
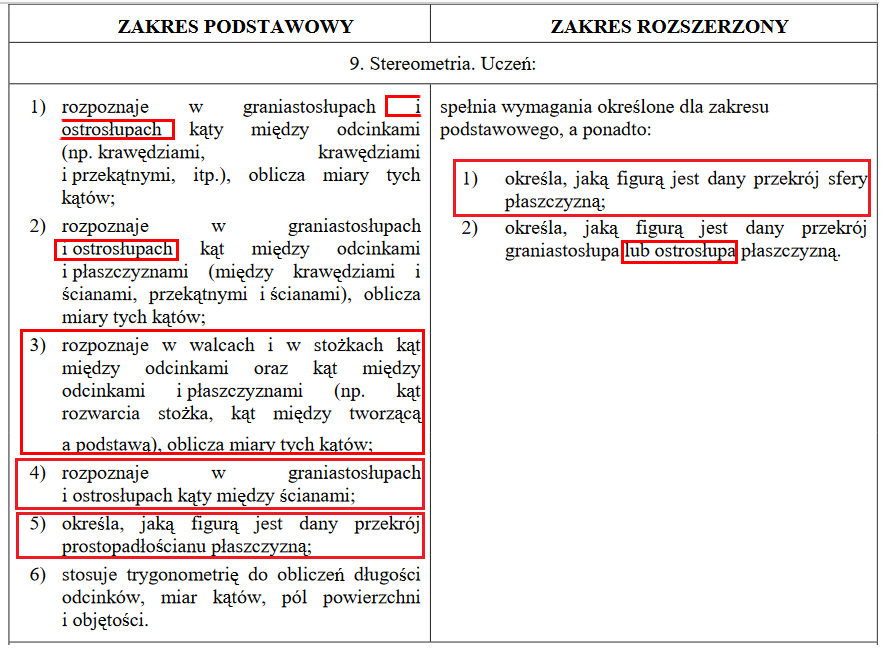
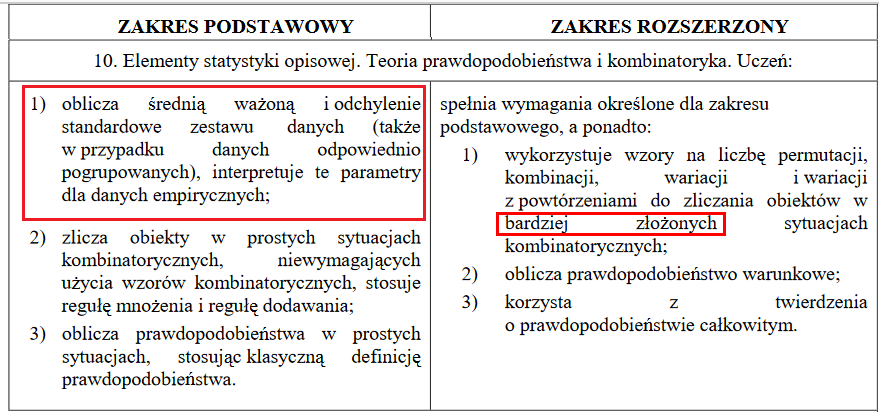
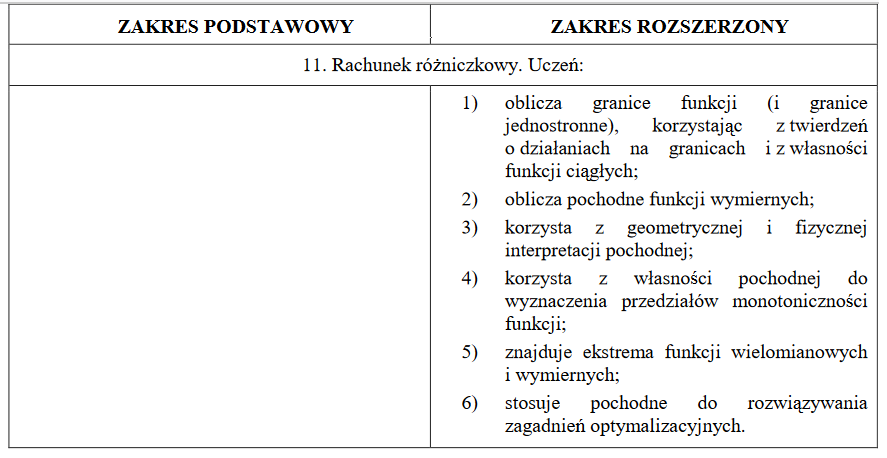
Matura z matematyki 2021.

Obraz może zawierać: tekst ?ZAKRES PODSTAWOWY 2. Wyrażenia algebraiczne. Uczeń: używa wzorów skróconego mnożenia na (a?b)2 oraz d-62. ZAKRES ROZSZERZONY na spełnia wymagania określone dla zakresu podstawowego, ponadto: 1) używa wzorów skróconego mnożenia (a+b) oraza+b; 2) dzieli wielomiany przez dwumian ax 3) rozkłada wielomian na czynniki, stosując wzory skróconego mnożenia lub wyłączając wspólny czynnik przed nawias; 4) dodaje, odejmuje mnoży wielomiany; 5) wyznacza dziedzinę prostego wyrażenia wymiernego jedną zmienną, w którym mianowniku występują tylko wyrażenia dające się łatwo sprowadzić do iloczynu wielomianów liniowych kwadratowych; 6) dodaje, odejmuje, mnoży dzieli wyrażenia wymierne; rozszerza (w łatwych przykładach) skraca wyrażenia wymierne.?

Matura z matematyki 2021.

Matura z matematyki 2021.

Matura z matematyki 2021.

Matura z matematyki 2021.

Matura z matematyki 2021.

Obraz może zawierać: tekst ?ZAKRES PODSTAWOWY ZAKRES ROZSZERZONY 10. Elementy statystyki opisowej. Teoria prawdopodobieństwa kombinatoryka. Uczeń: 2) oblicza średnią ważoną iodchylenie spełnia wymagania określone dla zakresu standardowe zestawu danych (także podstawowego, ponadto: w przypadku danych odpowiednio 1) wykorzystuje wzory na liczbę permutacji, pogrupowanych), interpretuje te parametry kombinacji, wariacji wariacji dla danych empirycznych; zpowtórzeniami do zliczania obiektów w bardziej złożonych sytuacjach kombinatorycznych; oblicza prawdopodobieństwo warunkowe; korzysta z twierdzenia prawdopodobieństwie całkowitym. zlicza obiekty w prostych sytuacjach kombinatorycznych, niewymagających użycia wzorów kombinatorycznych, stosuje regułę mnożenia regułę dodawania; 3) oblicza prawdopodobieństwa w prostych sytuacjach, stosując klasyczną definicję prawdopodobieństwa. 2) 3)?

Obraz może zawierać: tekst ?ZAKRES PODSTAWOWY ZAKRES ROZSZERZONY granice ztwierdzeń zwłasności 2) 3) 11. Rachunek różniczkowy. Uczeń: 1) oblicza granice funkcji jednostronne), korzystając o działaniach na granicach funkeji ciągłych; oblicza pochodne funkcji wymiernych; korzysta z geometrycznej fizycznej interpretacji pochodnej; korzysta z własności pochodnej do wyznaczenia przedziałów monotoniczności funkcji; znajduje ekstrema funkcji wielomianowych wymiernych; stosuje pochodne do rozwiązywania zagadnień optymalizacyjnych. 5) 6)?

 

 

Related Articles

Tablice wzorów do 2022

Informator maturalny od 2015 do 2022

Komisje egzaminacyjne

logo 2022 joomla footer

© 2022 Tomasz Grębski MATEMATYKA