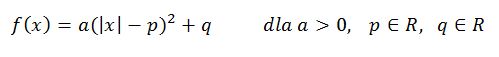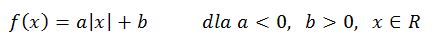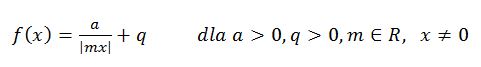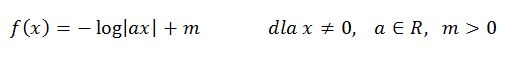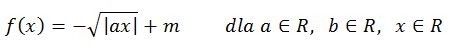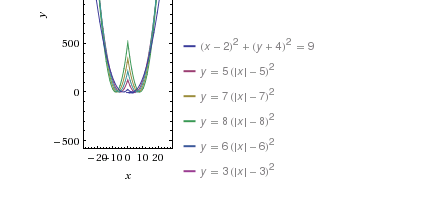Matematyczne choinki
Zapytacie o co tu chodzi? Przecież choinka, to drzewko, które kojarzy nam się ze świętami, prezentami, ale czy z matematyką? Chyba raczej nie:) Pokaże Wam, że można patrzeć na choinki w pełni matematycznie.
Jak stworzyć matematyczne choinki?
Czy można taką choinkę stworzyć przy użyciu funkcji czy krzywych matematycznych? Oczywiście, przecież matematyka jest wszędzie.
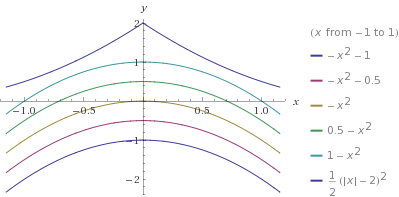
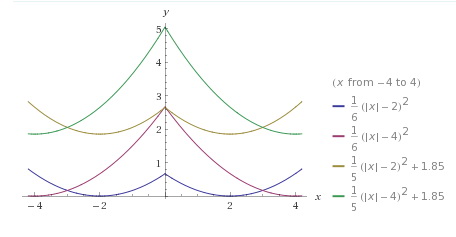
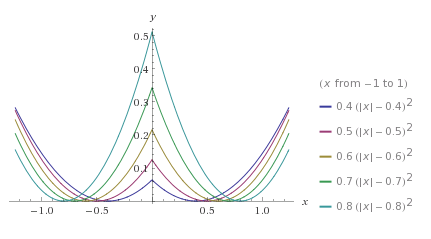
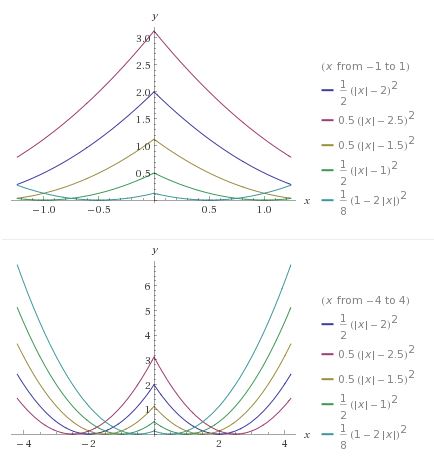
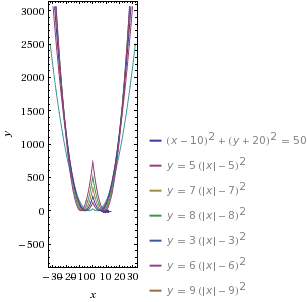
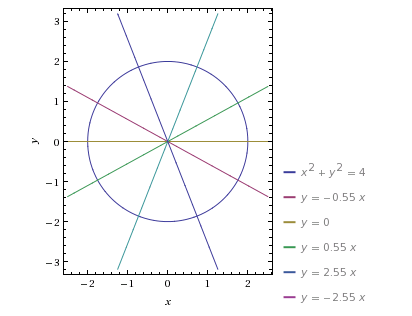
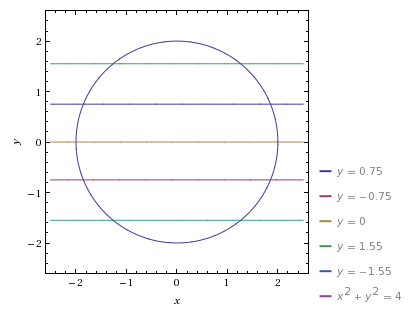
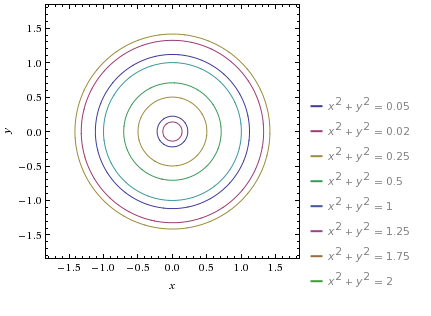
W celu narysowania poniższych wykresów można posłużyć się kilkoma popularnymi funkcjami z małą modyfikacją ich wzorów, tzn. wstawmy |x| w miejsce x. Zmiana ta spowoduje, że otrzymamy zawsze funkcje parzyste, czyli ich wykresy będą symetryczne względem osi OY.
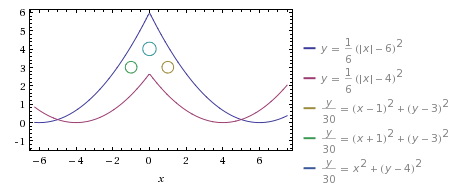
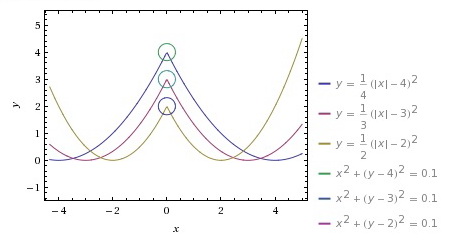
Zmieniając parametry we wzorach funkcji możemy ich wykresy przesuwać w dowolnym kierunku, kształtować ich wypukłości, odbijać symetrycznie, itp. Kolejną ważną sprawą jest podanie zakresu argumentów lub wartości funkcji w celu ograniczenia naszych gałązek, a dodając, np. równania okręgów można tworzyć matematyczne bombki na naszą choinkę.
Zaproponowałem moim uczniom stworzenie takich choinek, a że lubią wyzwania i mają odpowiednią wiedzę matematyczną, efekt jest świetny. Przy tej okazji również można wzbudzić zainteresowanie matematyką wśród uczniów.
Na początek moja własna twórczość:
|
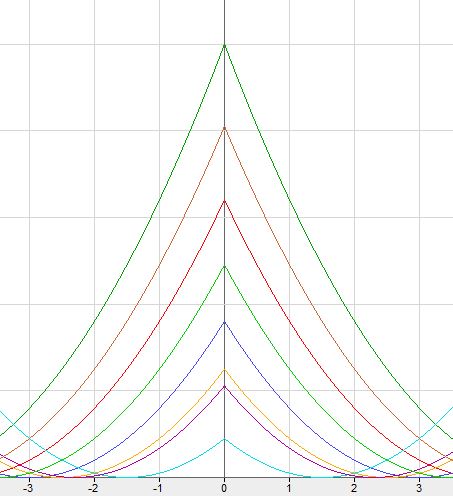
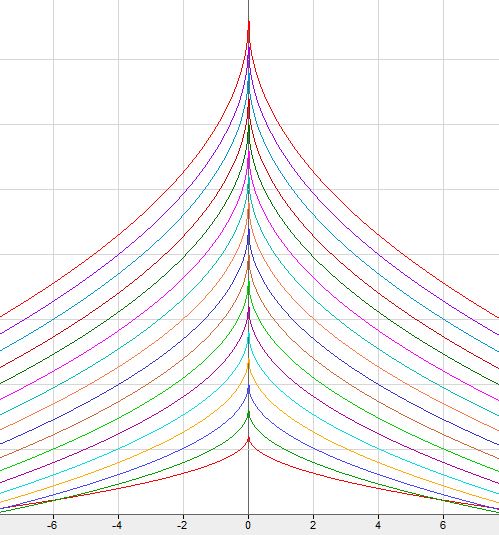
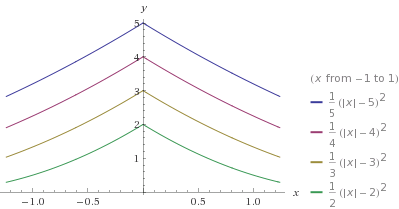
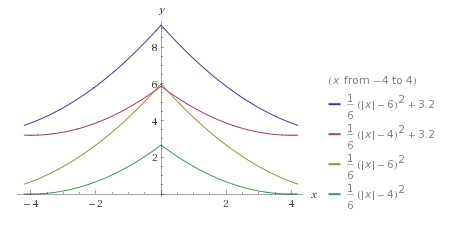
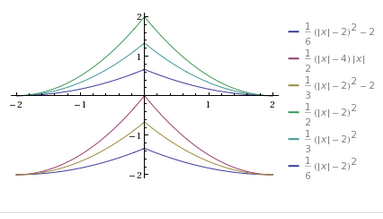
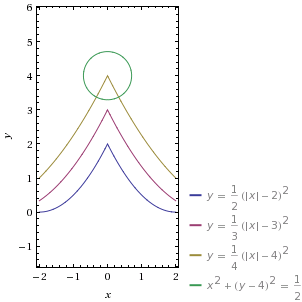
Choinka paraboliczna
|
|
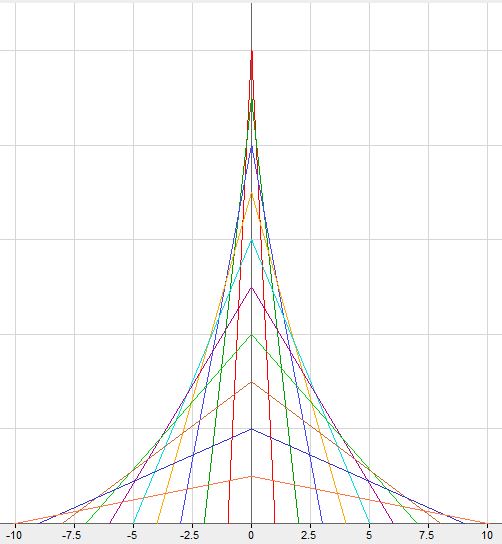
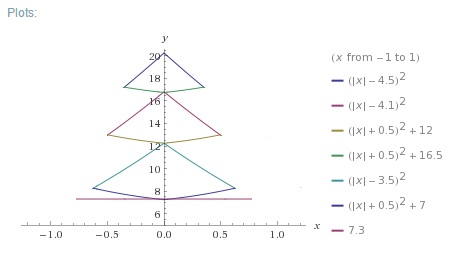
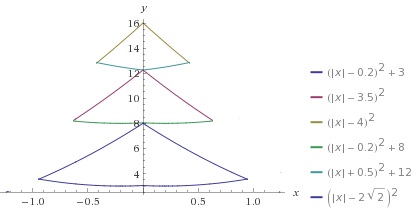
Choinka liniowa
|
|
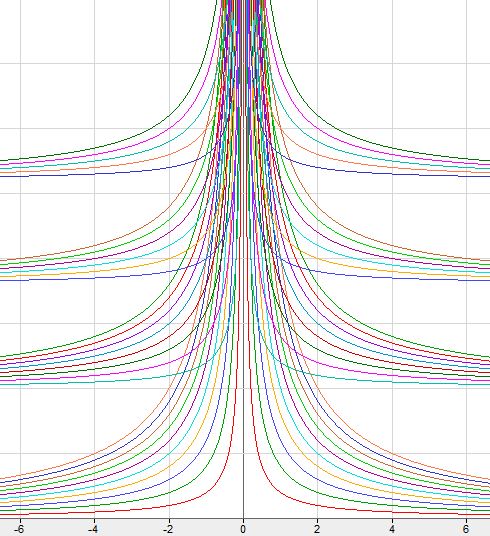
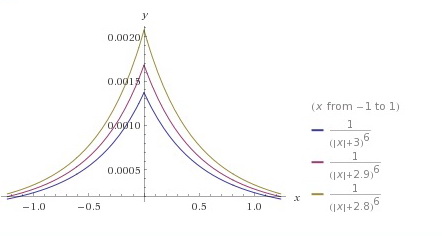
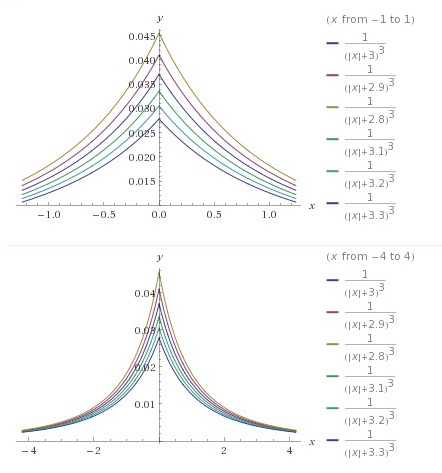
Choinka homograficzna (wymierna)
|
|
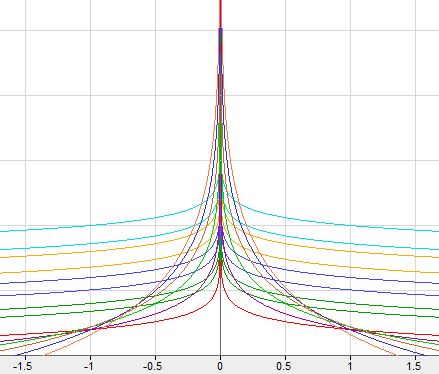
Choinka logarytmiczna
|
|
Choinka trygonometryczna
|
|
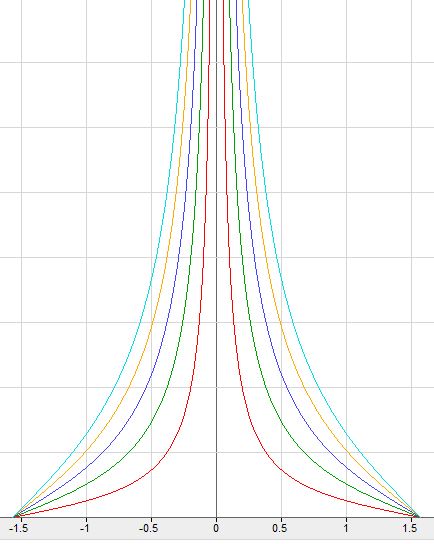
Choinka pierwiastkowa (niewymierna)
|
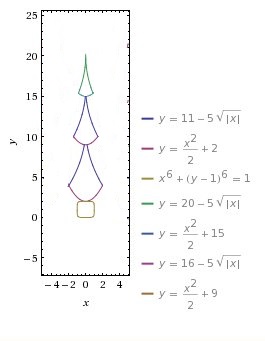
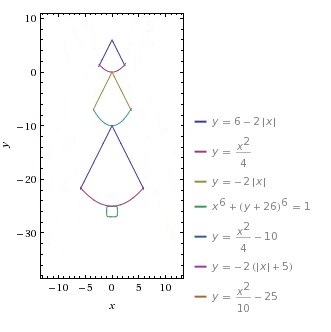
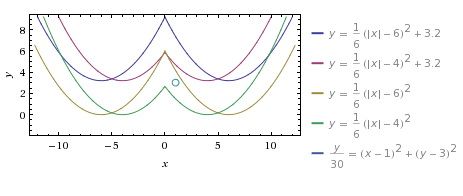
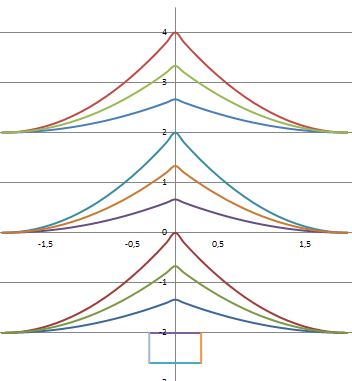
A teraz zobaczcie efekty pracy moich zdolnych uczniów:)
|
Autor: Angelika Zboch - klasa 2g
|
|
Autor: Damian Gnat - klasa 2e
|
|
Autor: Karolina Bryndza - klasa 2g
|
|
Autor: Małgorzata Tłuścik - klasa 2e
|
|
Autor: Monika Michałek - klasa 2e
|
|
Autor: Aleksandra Rębisz - klasa 3e
|
|
Autor: Patryk Kułaga - klasa 3e
|
|
Autor: Patryk Pielaszkiewicz - klasa 2g
|
|
Autor: Aleksandra Wronka - klasa 2g
|
|
Autor: Karol Wieczorek - klasa 3e
|
|
Autor: Alicja Mazurek - klasa 2g
|
|
Autor: Paulina Smołecka - klasa 2g Matematyczne bombki
|
To oczywiście nie jedyny sposób na narysowanie takich matematycznych choinek.
Pozostawiam czytelnikowi własną wyobraźnie i wiedzę matematyczną i zachęcam do matematyczno-świątecznej zabawy.
2014 Tomasz Grębski