WPROWADZENIE
Optymalizacja to proces poszukiwania najlepszego (optymalnego) rozwiązania problemu, np. poszukiwanie największego zysku, czy najmniejszego kosztu, próby zużycia najmniejszej ilości materiału przy produkcji pudełek lub największej powierzchni spełniającej dane warunki.
Jak rozpoznać zadanie optymalizacyjne?
To jest dość proste, ponieważ w treści takiego zadania będzie zapytanie o „coś” największego lub najmniejszego, np. jakie jest największe pole?; jaki jest największy zysk?
Wskazówki przy rozwiązywaniu zadań optymalizacyjnych na poziomie podstawowym (tzn. w przypadku, gdy otrzymujemy funkcję kwadratową):
1. Jeżeli zadanie dotyczy figury geometrycznej, to koniecznie narysuj rysunek wraz z oznaczeniami.
2. Utwórz funkcję, którą będziesz optymalizować (to ta wielkość, która ma być największa/najmniejsza)
3. Z treści zadania należy wydobyć związek między wielkościami występującymi we wzorze utworzonej funkcji i wyznaczyć jedną wielkość przy pomocy drugiej, aby po podstawieniu jej do wzoru funkcji otrzymać funkcję jednej zmiennej.
4. Pamiętaj o określeniu dziedziny. Jeśli np. wielkości występujące w zadaniu dotyczą wymiarów figury geometrycznej, to wymiary muszą być dodatnie.
5. Po utworzeniu i uporządkowaniu funkcji okaże się, że otrzymamy funkcję kwadratową.
6. Wystarczy teraz policzyć współrzędną p wierzchołka paraboli.
Poniżej przedstawiam 35 zadań, które przybliżą problem bardzo dokładnie.
Zadanie 1.
Daną liczbę rzeczywistą a przedstaw jako sumę dwóch takich liczb, aby suma kwadratów tych liczb była najmniejsza.
Załóżmy, że $$a=x+y$$. Zatem $$y=a-x$$. Stąd:
$$
x^2+y^2=x^2+(a-x)^2=x^2+a^2-2 a x+x^2=2 x^2-2 a x+a^2 .
$$
Niech $$f(x)=2 x^2-2 a x+a^2$$. Funkcja $$f$$ przyjmuje wartość najmniejszą dla:
$$
x=\frac{-(-2 a)}{2 \cdot 2}=\frac{a}{2} .
$$
Ponieważ $$y=a-x$$, więc $$y=\frac{a}{2}$$ (zatem liczby $$x$$ i $$y$$ są równe).
Odp.: $$x=\frac{a}{2}, y=\frac{a}{2}$$.
Uwaga: Skorzystaliśmy z faktu, że jeżeli $$a>0$$, to funkcja $$f(x)=a x^2+b x+c$$ przyjmuje wartość najmniejszą dla $$x=-\frac{b}{2 a}$$ (wartość ta jest równa $$\frac{-\Delta}{4 a}$$ ).
Zadanie 2.
Liczbę 8 przedstaw jako sumę takich dwóch składników, aby suma ich sześcianów była najmniejsza.
Zadanie 3.
Siatką drucianą długości $$60 \mathrm{~m}$$ należy ogrodzić prostokątny plac przylegający jednym bokiem do muru. Jakie wymiary winien mieć plac, aby jego pole było największe?
Zadanie 4.
Prostokąt ma boki długości $$a \mathrm{~cm}$$ i $$b \mathrm{~cm}$$. Bok $$a$$ powiększamy o $$x \mathrm{~cm}$$, zaś bok $$b$$ zmniejszamy o $$x \mathrm{~cm}$$. Dla jakiej wartości $$x$$ pole nowego prostokąta będzie najwieksze?
Zadanie 5.
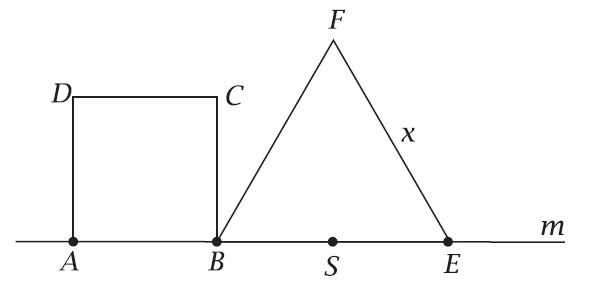
Dane są kwadrat $$A B C D$$ i trójkąt równoboczny $$B E F$$, którego bok ma długość $$x$$. Punkty $$A$$, $$B$$ i $$E$$ leżą na prostej $$m$$. Punkt $$S$$ jest środkiem odcinka $$B E$$ oraz długość odcinka $$A S$$ jest równa 2 (zobacz rysunek).
Wyznacz taką wartość $$x$$, dla której suma pól kwadratu $$A B C D$$ i trójkąta $$B E F$$ jest najmniejsza. Dla wyznaczonej wartości $$x$$ oblicz długość lamanej ADCBFE. Zapisz obliczenia.
Zadanie 6.
Dany jest prostokąt $$A B C D$$ o bokach długości 8 i 10 oraz odcinek o długości $$x$$. Rozważamy wszystkie prostokąty, które powstają z prostokąta $$A B C D$$ w ten sposób, że każdy krótszy bok tego prostokąta powiększymy o $$2 x$$, a każdy dłuższy bok zmniejszymy o $$x$$.
Podaj wzór i dziedzinę funkcji opisującej zależność pola tak zbudowanego prostokąta od $$x$$. Oblicz wymiary tego z rozważanych prostokątów, który ma największe pole, i oblicz to największe pole.
Zapisz obliczenia.
Zadanie 7.
Prostopadłościan o wysokości długości $$10 \mathrm{~cm}$$ ma w podstawie prostokąt o obwodzie $$24 \mathrm{~cm}$$. Objętość tego prostopadłościanu jest największa z możliwych.
Oblicz tę objętość. Zapisz swoje obliczenia.
Zadanie 8.
Przekrój osiowy walca ma obwód $$20 \mathrm{~cm}$$. Jak dobrać wymiary walca, aby pole jego powierzchni bocznej było najwiekksze?
Zadanie 9.
Przekrój osiowy stożka ma obwód $$30 \mathrm{~cm}$$. Czy można dobrać tak wymiary stożka, aby pole jego powierzchni bocznej było największe?
Zadanie 10.
Okno ma kształt prostokąta zakończonego na górze trójkątem równobocznym. Obwód okna wynosi p. Jaka powinna być podstawa prostokąta, aby powierzchnia okna była największa?
Zadanie 11.
Okno ma kształt prostokąta zakończonego na górze półkolem. Jaka powinna być podstawa prostokąta, aby przy obwodzie okna wynoszącym $$2 \mathrm{~m}$$ powierzchnia okna była największa?
Zadanie 12.
Z prostokątnego arkusza tektury o wymiarach $$30 \mathrm{~cm}$$ i $$50 \mathrm{~cm}$$ należy wyciąć w rogach kwadraty tak, aby po złożeniu otrzymać otwarte pudełko. Jak dobrać dlugość boku kwadratów, aby pole powierzchni bocznej pudelka było największe?
Zadanie 13.
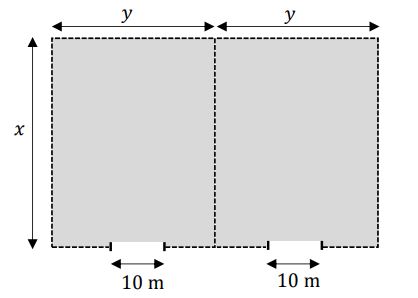
Powierzchnia magazynowa będzie się składała z dwóch identycznych prostokątnych działek połączonych wspólnym bokiem. Całość ma być ogrodzona płotem, przy czym obie działki będzie rozdzielał wspólny płot. W ogrodzeniu będą zamontowane dwie bramy wjazdowe, każda o szerokości 10 m (zobacz rysunek poniżej). Łączna długość płotu ogradzającego oraz rozdzielającego obie działki wyniesie 580 metrów, przy czym szerokości obu bram wjazdowych nie wliczają się w długość płotu.
Oblicz wymiary $$x$$ i $$y$$ każdej z dwóch prostokątnych działek, tak aby całkowite pole powierzchni magazynowej było największe.
Zadanie 14.
Rodzinna firma stolarska produkuje male wiatraki ogrodowe. Na podstawie analizy
rzeczywistych wpływów i wydatków stwierdzono, że:
- $$\quad$$ przychód $$P$$ (w złotych) z tygodniowej sprzedaży $$x$$ wiatraków można opisać funkcją $$P(x)=251 x$$
- koszt $$K$$ (w złotych) produkcji $$x$$ wiatraków w ciagu jednego tygodnia można określić funkcja $$K(x)=x^2+21 x+170$$.
Tygodniowo w zakładzie można wyprodukować co najwyżej 150 wiatraków.
Oblicz, ile tygodniowo wiatraków należy sprzedać, aby zysk zakładu w ciągu jednego tygodnia był największy. Oblicz ten największy zysk.
Zapisz obliczenia.
Wskazówka: przyjmij, że zysk jest różnicą przychodu i kosztów.
Zadanie 15.
Rozważamy wszystkie równoległoboki o obwodzie równym 200 i kącie ostrym o mierze $$30^{\circ}$$.
Podaj wzór i dziedzinę funkcji opisującej zależność pola takiego równoległoboku od długości $$x$$ boku równoległoboku.
Oblicz wymiary tego z rozważanych równoległoboków, który ma największe pole, i oblicz to największe pole.
Zadanie 16.
Firma handlowa ustaliła, że liczba sprzedanych przez nią egzemplarzy gry komputerowej w ciągu każdego tygodnia zależy od jej ceny. Liczbę sprzedanych egzemplarzy opisuje funkcja $$f(x)=2400-15 x$$, gdzie $$x$$ oznacza cenę jednostkową gry.
Jaka powinna być cena jednostkowa, aby tygodniowy przychód $$P$$ ze sprzedaży gry był największy? Oblicz ten największy przychód.
Zapisz obliczenia.
Wskazówka: przyjmij, że przychód jest iloczynem liczby sprzedanych gier oraz ceny jednostkowej tej gry.
Zadanie 17.
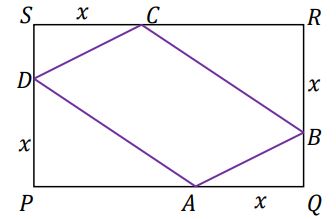
Dany jest prostokąt $$P Q R S$$ o bokach długości $$|P Q|=|S R|=10$$ oraz $$|P S|=|Q R|=6$$.
Na bokach $$P Q, Q R, R S, S P$$ obrano odpowiednio punkty $$A, B, C, D$$ takie, że
$$|A Q|=|B R|=|C S|=|D P|=x$$ oraz $$x \geq 3$$ (zobacz rysunek).
Wyznacz długość odcinka $$x$$, dla którego pole czworokąta $$A B C D$$ jest najmniejsze.
Wyznacz to pole. Zapisz obliczenia.
Zadanie 18.
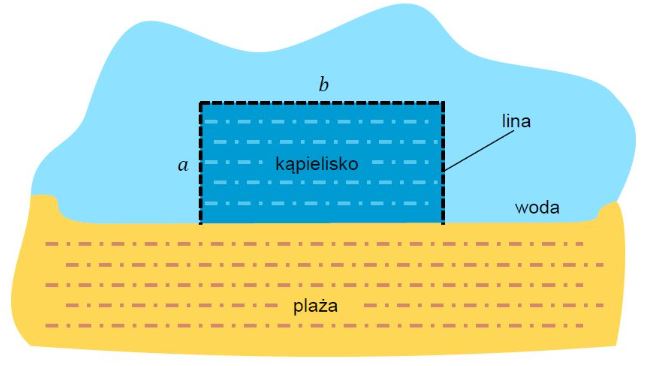
Do wyznaczenia trzech boków pewnego kąpieliska w kształcie prostokąta należy użyć liny o długości 200 m. Czwarty bok tego kąpieliska będzie pokrywał się z brzegiem plaży, który w tym miejscu jest linią prostą (zobacz rysunek).
Oblicz wymiary $$a$$ i $$b$$ kąpieliska tak, aby jego powierzchnia była największa.
Zapisz obliczenia.
Zadanie 19.
Sklep sprowadza z hurtowni kurtki płacąc po 100 zl za sztukę i sprzedaje średnio 40 sztuk miesięcznie po 160 zł. Zaobserwowano, że każda kolejna obniżka ceny sprzedaży kurtki o 1 zl zwiększa sprzedaż miesięczną o 1 sztukę. Jaką cenę kurtki powinien ustalić sprzedawca, aby jego miesięczny zysk był największy?
Zadanie 20.
Suma trzech liczb rzeczywistych dodatnich jest równa 13. Druga liczba jest trzy razy większa od pierwszej. Wyznacz trzy liczby spetniające podane warunki tak, aby suma ich kwadratów była najmniejsza.
Zadanie 21.
Wyznacz taki punkt $$A$$ na prostej $$2 x+y-1=0$$, by suma kwadratów jego odległości od osi układu była najmniejsza.
Zadanie 22.
Bok kwadratu $$A B C D$$ ma długość 1 . Na bokach $$B C$$ i $$C D$$ wybrano odpowiednio punkty $$E$$ i $$F$$ umieszczone tak, by $$|C E|=2|D F|$$. Oblicz wartość $$x=|D F|$$, dla której pole trójkąta $$A E F$$ jest najmniejsze.
Zadanie 23.
Dane są punkty $$A=(1,5), B=(9,3)$$ i prosta $$k$$ o równaniu $$y=x+1$$. Oblicz wspólrzędne punktu $$C$$ leżącego na prostej $$k$$, dla którego suma $$|A C|^2+|B C|^2$$ jest najmniejsza.
Zadanie 24.
Dany jest kwadrat $$A B C D$$ o boku równym $$2 . \mathrm{Na}$$ bokach $$B C$$ i $$C D$$ wybrano odpowiednio punkty $$E$$ i $$F$$, różne od wierzchołków kwadratu, takie że $$|C E|=|D F|=x$$. Oblicz wartość $$x$$, dla której pole trójkąta $$A E F$$ jest najmniejsze i oblicz to pole.
Zadanie 25.
Wśród wszystkich graniastosłupów prawidłowych sześciokątnych, w których suma długości wszystkich krawędzi jest równa 24, jest taki, który ma największe pole powierzchni bocznej. Oblicz długość krawędzi podstawy tego graniastosłupa.
Zadanie 26.
Na płaszczyźnie dane są punkty $$A=(3,-2)$$ i $$B=(11,4)$$. Na prostej o równaniu $$y=8 x+10$$ znajdź punkt $$P$$, dla którego suma $$|A P|^2+|B P|^2$$ jest najmniejsza.
Zadanie 27.
W układzie współrzędnych rozważmy wszystkie punkty $$P$$ postaci: $$\quad P=\left(\frac{1}{2} m+\frac{5}{2}, m\right)$$ gdzie $$m \in\langle-1,7\rangle$$. Oblicz najmniejszą i największą wartość $$|P Q|^2$$, gdzie $$Q=\left(\frac{55}{2}, 0\right)$$.
Zadanie 28.
Suma długości dwóch boków trójkąta równa się 4, a kąt między tymi bokami ma miarę $$120^{\circ}$$. Oblicz najmniejszą wartość sumy kwadratów długości wszystkich boków tego trójkąta.
Zadanie 29.
Dany jest odcinek $$A B$$ o długości 10 . Rozpatrujemy wszystkie sześciokąty foremne $$A C D M E F$$ i trójką̨y równoboczne $$M B G$$, których wspólny wierzchołek $$M$$ leży na odcinku $$A B$$.
Zadanie 30.
Dany jest kwadrat $$A B C D$$ o boku długości 2 . Na bokach $$B C$$ i $$C D$$ tego kwadratu wybrano - odpowiednio - punkty $$P$$ i $$Q$$, takie, że długość odcinka $$|P C|=|Q D|=x$$. Wyznacz tę wartość $$x$$, dla której pole trójkąta $$A P Q$$ osiąga wartość najmniejszą. Oblicz to najmniejsze pole.
Zadanie 31.
W pewnej firmie zależność przychodów ze sprzedaży od wielkości produkcji wyraża wzór $$p(n)=150 n$$, gdzie $$n$$ oznacza liczbę sztuk wyprodukowanego towaru, a koszty produkcji, w złotych, określa zależność $$k(n)=n^2+50 n+1600$$.
a) Wyznaczwzór funkcji z(n) - zależności zysku zakładu od wielkości produkcji, jeśli wiadomo, że zysk jest różnicą między przychodem zakładu a kosztami produkcji.
b) Przy jakiej wielkości produkcji zysk wynosi 0?
c) Jaka wielkość produkcji zapewnia największy zysk? Jaki jest koszt produkcji, gdy zysk jest największy?
Zadanie 32.
Liczbę 80 przedstaw w postaci różnicy dwóch liczb tak, aby suma ich kwadratów była najmniejsza.
Zadanie 33.
Liczbę 24 przedstaw w postaci sumy dwóch liczb tak, aby suma kwadratu podwojonej jednej liczby i kwadratu drugiej liczby była najmniejsza.
Zadanie 34.
Rozpatrujemy trójkąty równoramienne, w których suma długości podstawy i wysokości opuszczonej na tę podstawę jest równa $$12 \mathrm{~cm}$$. Wyznacz długości boków trójkąta mającego największe pole.
Zadanie 35.
Rzucono kamień pionowo w górę z prędkością początkową $$12 \mathrm{~m} / \mathrm{s}$$. Zależność między wysokością S kamienia liczoną w metrach, a czasem $$t$$ liczonym w sekundach, wyraża wzór funkcji $$S(t)=12 t-5 t^2$$. Podaj dziedzinę tej funkcji. Jaką największą wysokość osiągnie ten kamień?