Zadanie 1
Rozwiąż równanie: \(2 x^4-9 x^3+14 x^2-9 x+2=0\).
Rozwiązanie:
Większość rozwiązujących zacznie od szukania całkowitego lub wymiernego pierwiastka równania. Szybko taki pierwiastek się znajdzie, jednak chciałbym przedstawić inny sposób rozwiązania, bo nie zawsze sytuacja jest tak prosta. Zwróćmy uwagę na symetrycznie rozmieszczone współczynniki tego równania. Takie równanie nazywamy równaniem symetrycznym. Sposób rozwiązania jest następujący: obie strony równania trzeba podzielić przez środkową potęgę, czyli w tym wypadku - przez \(x^2\). Możemy to zrobić, ponieważ \(x^2=0\) nie jest pierwiastkiem tego równania.
\(2 x^4-9 x^3+14 x^2-9 x+2=0 \quad:: x^2\)
\(2 x^2-9 x+14-\frac{9}{x}+\frac{2}{x^2}=0\)
Odpowiednio pogrupujemy wyrazy.
(*) \(2\left(x^2+\frac{1}{x^2}\right)-9\left(x+\frac{1}{x}\right)+14=0\)
Skorzystamy teraz ze wzoru skróconego mnożenia:
\((a+b)^2=a^2+2 a b+b^2 \Rightarrow a^2+b^2=(a+b)^2-2 a b\)
Wobec tego
\(x^2+\frac{1}{x^2}=\left(x+\frac{1}{x}\right)^2-2 \cdot x \cdot \frac{1}{x}=\left(x+\frac{1}{x}\right)^2-2\)
Podstawiamy to wyrażenie do równania \((*)\) :
\(2\left[\left(x+\frac{1}{x}\right)^2-2\right]-9\left(x+\frac{1}{x}\right)+14=0\)
Wprowadzamy nową zmienną.
\(x+\frac{1}{x}=t\), gdzie \(t \in \boldsymbol{R}\)
A więc
\(\begin{aligned}&2\left[t^2-2\right]-9 t+14=0 \\&2 t^2-9 t+10=0 \\&\Delta=1, \sqrt{\Delta}=1\end{aligned}\)
\(\left(t=2 \vee t=\frac{5}{2}\right) \wedge x+\frac{1}{x}=t\)
Wracamy do pierwotnej zmiennej.
\(x+\frac{1}{x}=2 \vee x+\frac{1}{x}=\frac{5}{2} \quad \quad\)
Mnożymy obie strony obu równań przez \(x\).
\(x^2-2 x+1=0 \vee 2 x^2-5 x+2=0 \quad\)
\(x=1 \vee x=2 \vee x=\frac{1}{2}\)
Odpowiedź: \(x \in\left\{\frac{1}{2}, 1,2\right\}\)
Zadanie 2
Rozwiąż równanie: \(x^6-12 x^5+50 x^4-84 x^3+50 x^2-12 x+1=0\).
Rozwiązanie:
Oto kolejne równanie symetryczne. Tym razem równanie nie ma pierwiastków wymiernych.
Podobnie jak w zadaniu poprzednim, podzielimy obie strony równania przez środkową potęgę, czyli przez \(x^3(x=0\) nie jest pierwiastkiem tego równania).
\(x^6-12 x^5+50 x^4-84 x^3+50 x^2-12 x+1=0 \quad /: x^3\)
\(x^3-12 x^2+50 x-84+\frac{50}{x}-\frac{12}{x^2}+\frac{1}{x^3}=0\)
Odpowiednio pogrupujmy wyrazy.
\((*)\left(x^3+\frac{1}{x^3}\right)-12\left(x^2+\frac{1}{x^2}\right)+50\left(x+\frac{1}{x}\right)-84=0\)
Skorzystamy ze wzorów skróconego mnożenia:
\(\begin{aligned}&(a+b)^3=a^3+3 a^2 b+3 a b^2+b^3 \Rightarrow a^3+b^3=(a+b)^3-3 a b(a+b) \\&(a+b)^2=a^2+2 a b+b^2 \Rightarrow a^2+b^2=(a+b)^2-2 a b\end{aligned}\)
A zatem
\(\begin{aligned}&x^3+\frac{1}{x^3}=\left(x+\frac{1}{x}\right)^3-2 \cdot x \cdot \frac{1}{x} \cdot\left(x+\frac{1}{x}\right)-2=\left(x+\frac{1}{x}\right)^3-3\left(x+\frac{1}{x}\right) \\&x^2+\frac{1}{x^2}=\left(x+\frac{1}{x}\right)^2-2 \cdot x \cdot \frac{1}{x}=\left(x+\frac{1}{x}\right)^2-2\end{aligned}\)
Te wyrażenia podstawiamy do równania \((*)\).
\(\left(x+\frac{1}{x}\right)^3-3\left(x+\frac{1}{x}\right)-12\left[\left(x+\frac{1}{x}\right)^2-2\right]+50\left(x+\frac{1}{x}\right)-84=0\)
Wprowadzamy nową zmienną.
\(x+\frac{1}{x}=t\), gdzie \(t \in \boldsymbol{R}\)
A więc
\(\begin{aligned}&t^3-3 t-12\left[t^2-2\right]+50 t-84=0 \\&t^3-12 t^2+47 t-60=0\end{aligned}\)
Aby rozwiązać powyższe równanie, poszukajmy pierwiastków wśród dzielników wyrazu wolnego wielomianu występującego po lewej stronie. Zbiór dzielników 60 to \(\{\pm 1, \pm 2, \pm 3, \pm 4\), \(\pm 5, \pm 6, \pm 12, \pm 15, \pm 20, \pm 30, \pm 60\}\).
Szybko zauważymy, że \(W(3)=0\). Na podstawie twierdzenia Bézouta wiemy zatem, że wielomian \(W(t)=t^3-12 t^2+47 t-60\) dzieli się przez dwumian \((t-3)\). Przy dzieleniu zastosujemy schemat Hornera.
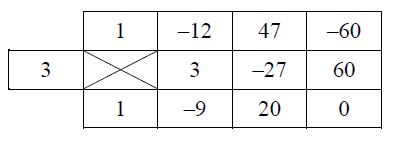
Mamy zatem \((t-3)\left(t^2-9 t+20\right)=0\)
Obliczając pierwiastki wyrażenia kwadratowego \(t^2-9 t+20\), otrzymujemy ostatecznie postać iloczynową równania \((t-3)(t-4)(t-5)=0\), czyli \((t=3 \vee t=4 \vee t=5) \wedge x+\frac{1}{x}=t\)
Wracamy do zmiennej \(x\)
\(x+\frac{1}{x}=3 \vee x+\frac{1}{x}=4 \vee x+\frac{1}{x}=5 \quad\)
Mnożymy obie strony powyższych równań przez \(x\) i po uporządkowaniu otrzymujemy:
\(x^2-3 x+1=0 \quad \vee \quad x^2-4 x+1=0 \quad \vee \quad x^2-5 x+1=0\)
\(\Delta=5, \sqrt{\Delta}=\sqrt{5} \quad \Delta=12, \sqrt{\Delta}=2 \sqrt{3} \quad \Delta=21, \sqrt{\Delta}=\sqrt{21}\)
\(x=\frac{3-\sqrt{5}}{2} \vee x=\frac{3+\sqrt{5}}{2} \quad x=2-\sqrt{3} \vee x=2+\sqrt{3} \quad x=\frac{5-\sqrt{21}}{2} \vee x=\frac{5+\sqrt{21}}{2}\)
Odpowiedź: \(x \in\left\{\frac{3-\sqrt{5}}{2}, \frac{3+\sqrt{5}}{2}, 2-\sqrt{3}, 2+\sqrt{3}, \frac{5-\sqrt{21}}{2}, \frac{5+\sqrt{21}}{2}\right\}\).
Więcej ciekawych zadań w mojej książce - zbiorze zadań:
Podstawianie zmiennej pomocniczej w równaniach i nie tylko. Zadania z rozwiązaniami



