Zadanie 1.
W kulę o promieniu \(R\) wpisano cztery jednakowe kule wzajemnie do siebie styczne. Oblicz promień kul wpisanych.
Rozwiązanie:
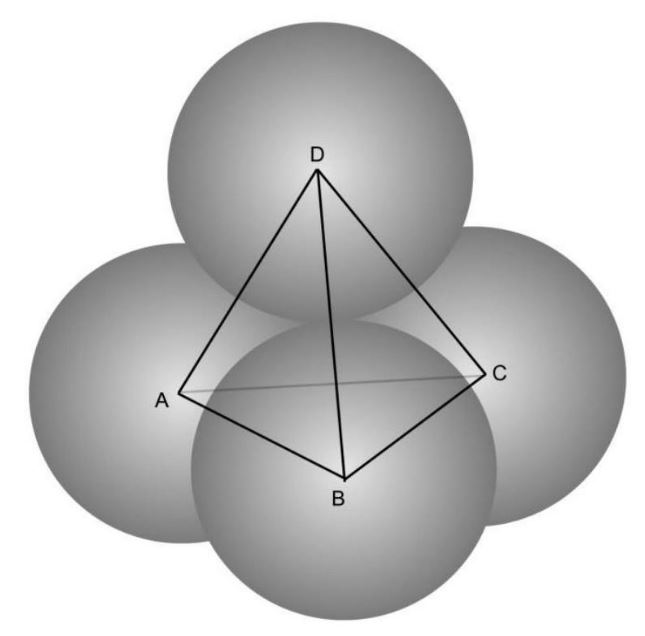
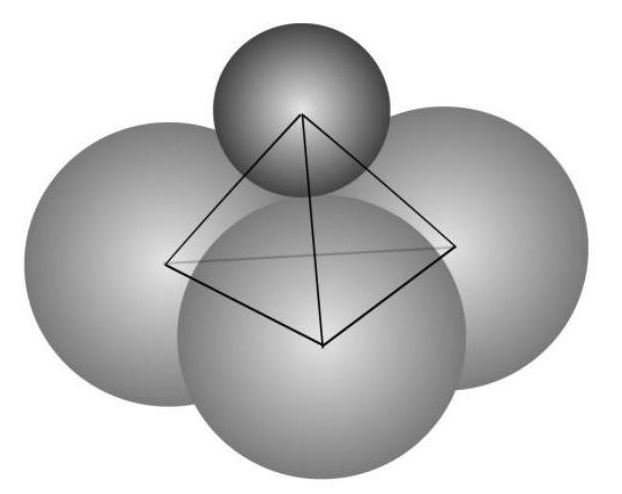
Na początek trzeba sobie wyobrazić jak te obiekty są położone. To chyba najtrudniejsza część zadania. Środki czterech kul są wierzchołkami czworościanu foremnego o boku długości \(2 r\), gdzie \(r\) - to promień wpisanych kul. Kule tworzą taką mała piramidę, co pokazuje rysunek 1.
Rysunek 1.
Krawędzie czworościanu mają długość \(2 r\). Wysokość wszystkich ścian czworościanu foremnego (są nimi trójkąty równoboczne) oznaczmy przez \(h\), zatem mamy \(h=\frac{2 r \sqrt{3}}{2}=r \sqrt{3}\).
Rysunek 2.
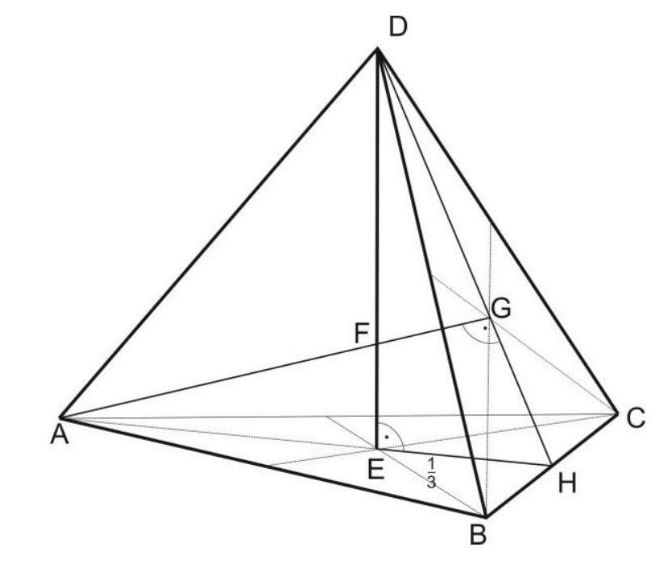
Wiemy również, że wysokości w trójkącie równobocznym przecinają się w stosunku \(2: 1\). Wykorzystując dodatkowo tw. Pitagorasa mamy (rysunek 2):
\[
H^{2}+\left(\frac{1}{3} r \sqrt{3}\right)^{2}=(r \sqrt{3})^{2}
\]
Z równania tego obliczamy \(H\) :
\[
H=\frac{2 \sqrt{6}}{3} r
\]
Punkt przecięcia się wysokości czworościanu foremnego będzie środkiem kuli opisanej na tym czworościanie, a także środkiem kuli opisanej na tych czterech kulach. Udowodnimy teraz twierdzenie:
Twierdzenie
Wysokości w czworościanie foremnym przecinają się w jednym punkcie, który dzieli je w stosunku 1:3.
Założenie:
Rysunek 3.
Teza: \(\frac{|F E|}{|F D|}=\frac{1}{3}\)
Dowód:
Na podstawie rysunku 3.
\(|G H|=\frac{1}{3} h\)
\(|A H|=h\)
\(\triangle A G H \sim \triangle A E F(k k)\)
Zatem
\(\frac{|F E|}{|A F|}=\frac{|G H|}{|A H|}=\frac{1}{3}\)
\(\triangle A F E \equiv \triangle F G D(k b k)\)
Zatem
\(\frac{|F E|}{|F D|}=\frac{1}{3}\)
c.n.d.
Promień sfery opisanej na czworościanie będzie równy \(\frac{3}{4} H\), a zatem promień sfery opisanej na kulach będzie równy:
\(R=\frac{3}{4} H+r\)
\(R=\frac{3}{4} \cdot \frac{2 \sqrt{6}}{3} r+r\)
\(R=\left(\frac{\sqrt{6}}{2}+1\right) r\)
Wyliczając \(r\) i pozbywając się niewymierności otrzymujemy ostateczną odpowiedź:
\(r=R(\sqrt{6}-2)\)
Zadanie 2.
Do naczynia w kształcie półkuli o danym promieniu \(R\) włożono 4 jednakowe kule. Okazało się, że płaska pokrywa naczynia jest styczna do każdej z tych kul. Oblicz promień kul umieszczonych w naczyniu.
Rozwi azanie:
Podobnie jak w poprzednim zadaniu należy wyobrazić sobie całą sytuację. Rysunki w tym pomogą:
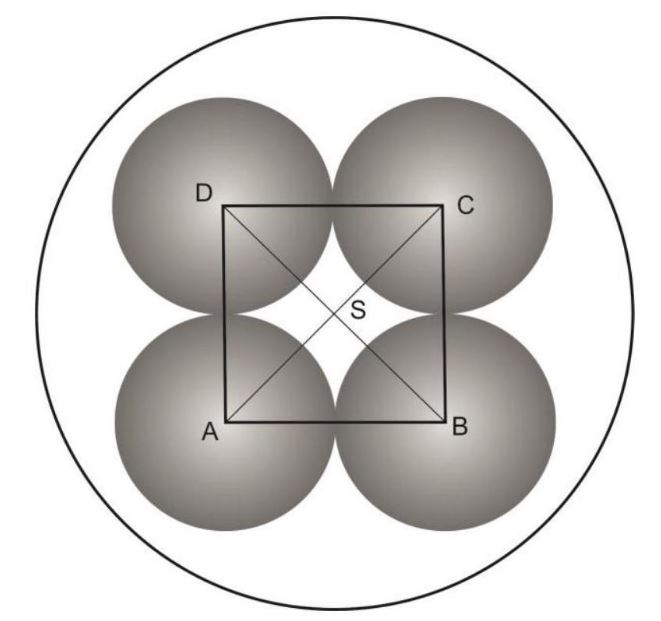
Rysunek 4. Widok z góry.
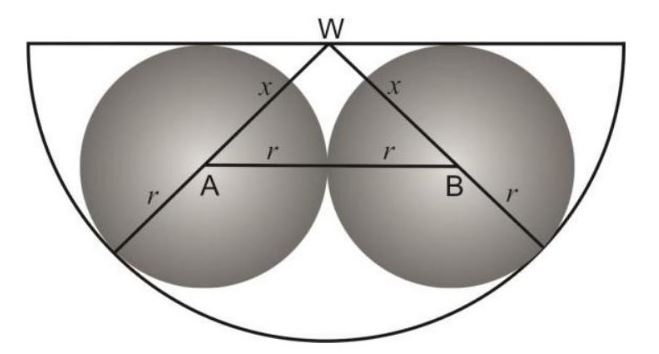
Rysunek 5. Widok z przodu.
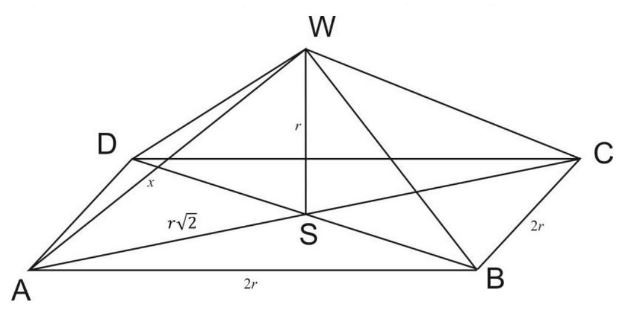
Widzimy na rysunku 4, że środki czterech kul umieszczonych w naczyniu i środek pokrywy tworzą ostrosłup prawidłowy czworokątny. W podstawie mamy kwadrat o boku długości \(2 r\), wysokości \(r\) oraz krawędzi bocznej \(x\). (rysunek 6)
Rysunek 6. Ostrosłup utworzony przez środki czterech kul oraz środek półkuli.
Korzystając \(z\) twierdzenia Pitagorasa wyznaczamy \(x\) za pomocą \(r\), czyli
\(r^{2}+(r \sqrt{2})^{2}=x^{2}\)
Stąd
\(x=\sqrt{3} r\)
Promień półkuli (rysunek 5)
\(R=x+r=\sqrt{3} r+r\)
Stąd otrzymujemy odpowiedź: \(r=\frac{R}{\sqrt{3}+1}\)
Zadanie 3.
Z czterech kul trzy mają promień \(R\), czwarta zaś \(r\). Z tych kul ustawiono na stole piramidę tak, że każda z tych kul jest styczna do trzech pozostałych, przy czym kule jednakowe tworzą jej podstawę. Oblicz największą odległość punktów kuli o promieniu \(r\) od blatu stołu oraz podaj warunek jaki muszą spełniać promienie, aby ustawienie piramidy było możliwe.
Rozwiązanie:
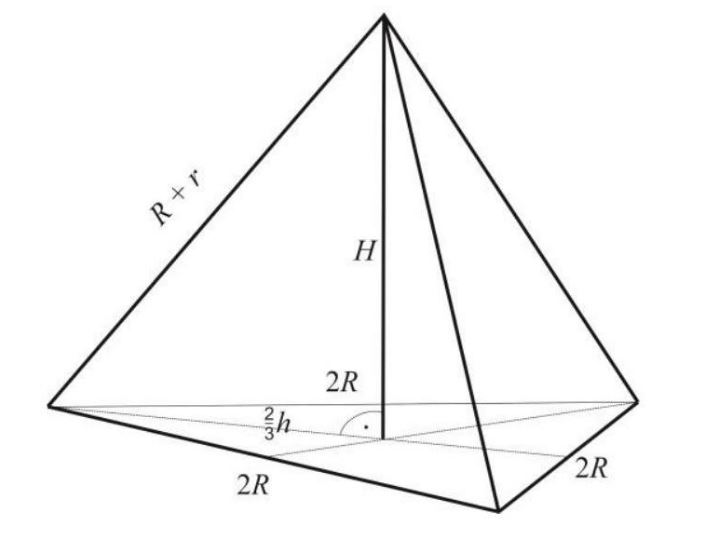
Środki kul tworzą ostrosłup prawidłowy trójkątny, w którym krawędź podstawy wynosi \(2 R\).
Rysunek 7. Widok poglądowy.
Spodek wysokości ostrosłupa jest punktem przecięcia wysokości podstawy, które dzielą się w stosunku 2:1.
Rysunek 8.
Wyznaczamy:
\(\frac{2}{3} h=\frac{2}{3} \cdot \frac{2 R \sqrt{3}}{2}=\frac{2 R \sqrt{3}}{3}\)
Korzystając z tw. Pitagorasa wyznaczamy \(H\) :
\(H^{2}+\left(\frac{2 R \sqrt{3}}{3}\right)^{2}=(R+r)^{2}\)
\(H^{2}=R^{2}+2 R r+r^{2}-\frac{4 R^{2}}{3}\) \(H=\sqrt{2 R r+r^{2}-\frac{R^{2}}{3}}\)
Największą odległością (oznaczmy \(d\) ) punktów kuli o promieniu \(r\) od blatu stołu będzie suma:
\(d=H+R+r\)
Zatem mamy:
\(d=\sqrt{2 R r+r^{2}-\frac{R^{2}}{3}}+R+r\)
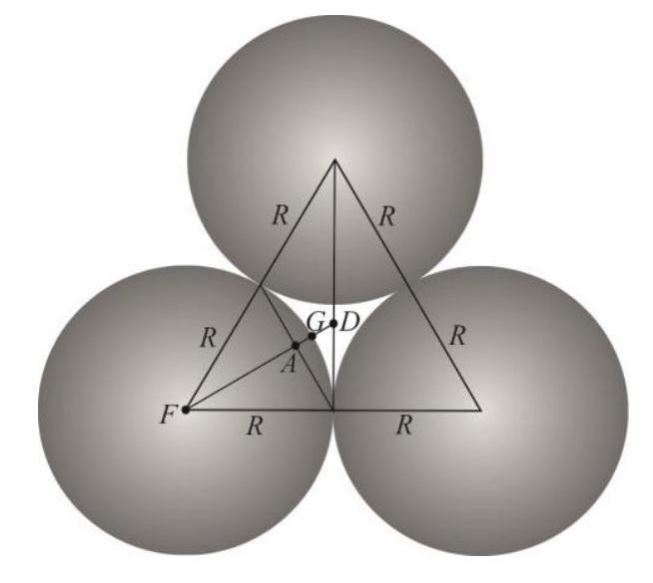
Zbadajmy teraz, kiedy ustawienie takiej piramidy będzie możliwe? Będzie to wtedy, gdy kula o promieniu \(r\), nie wpadnie” między kule o promieniu \(R\).
Rysunek 9. Widok z góry.
\[
\begin{aligned}
&|F A|=\frac{R \sqrt{3}}{2} \\
&|F G|=R \\
&|F D|=\frac{2}{3} \cdot \frac{2 R \sqrt{3}}{2}=\frac{2 R \sqrt{3}}{3} \\
&x=|F D|-|F G|=\frac{2 R \sqrt{3}}{2}-R
\end{aligned}
\]
Aby kula o promieniu \(r\) nie wpadła między pozostałe trzy kule o promieniach \(R\), jej promień musi być większy niż różnica \(x\), czyli
\(r>\frac{2 R \sqrt{3}}{2}-R\)
Zadanie 4.
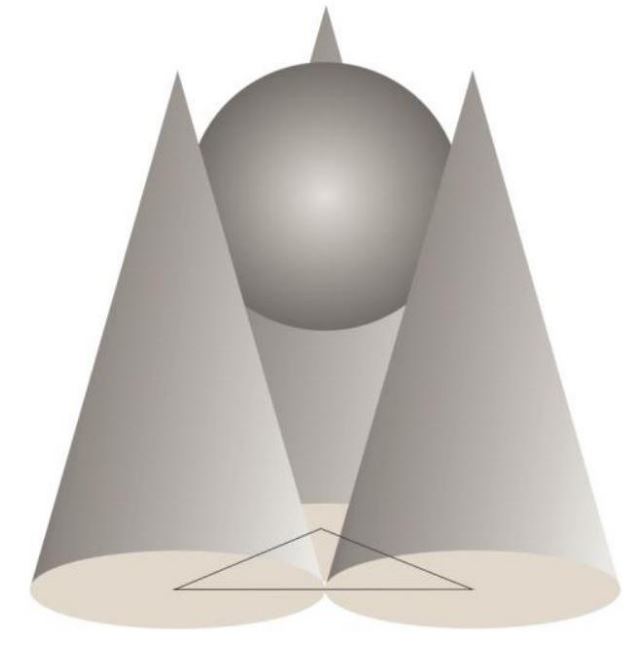
Na stole stoją trzy jednakowe stożki o parami stycznych podstawach, pomiędzy którymi umieszczono kulę. Kula jest takiej wielkości, że jej najwyższy punkt leży na tej samej wysokości co wierzchołki stożków. Jaki jest promień kuli, jeśli podstawa stożków ma promień równy 50 , a ich wysokość wynosi 120 ?
Rozwiązanie:
Rysunek 10 . Widok poglądowy.
Środki podstaw stożków są wierzchołkami trójkąta równobocznego o boku długości 100.
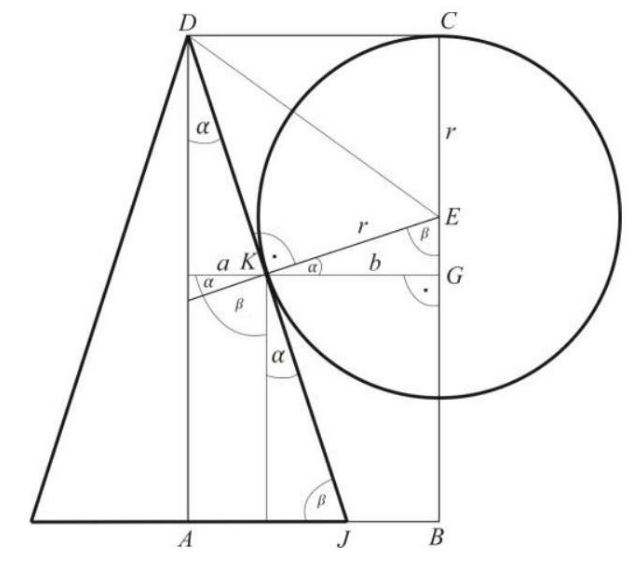
W prowadźmy oznaczenia: punkt \(B\) jest punktem, w którym przecinają się wysokości trójkąta równobocznego w znanym stosunku 2:1. Punk \(A\) to środek podstawy stożka, \(D\) to wierzchołek stożka, a punkt \(C\) to najwyższy punkt kuli (rysunek 11).
Rysunek 11. Widok przekroju.
Oznaczmy również
\(|A D|=H=120\)
\(|A J|=R=50\)
Z twierdzenia Pitagorasa obliczamy długość tworzącej stożka
\(|D J|=\sqrt{120^{2}+50^{2}}=130\)
Odległość \(|A D|\) to \(\frac{2}{3}\) wysokości trójkąta, którego wierzchołkami są środki podstaw stożków.
\(|A B|=\frac{2}{3} \cdot \frac{100 \sqrt{3}}{2}=\frac{100 \sqrt{3}}{3}\)
\(|A B|=|D C|=\frac{100 \sqrt{3}}{3}\) Trójkąty \(D C E\) i \(D E K\) są przystające \((b k b)\), zatem
\[
|D K|=\frac{100 \sqrt{3}}{3}
\]
Trójkąty \(A J D\) i \(K G E\) są podobne ( \(k k)\), zatem
\[
\frac{a}{|A J|}=\frac{|D K|}{|D J|}
\]
Podstawiając poprzednie obliczenia mamy
\[
\frac{\mathrm{a}}{50}=\frac{\frac{100 \sqrt{3}}{3}}{130}
\]
Stąd
\[
\begin{aligned}
&a=\frac{500 \sqrt{3}}{39} \\
&b=|A B|-a=\frac{100 \sqrt{3}}{3}-\frac{500 \sqrt{3}}{39}=\frac{800 \sqrt{3}}{39} \\
&\frac{b}{|A D|}=\frac{r}{|D J|}
\end{aligned}
\]
Stąd otrzymujemy odpowiedź
\[
r=\frac{800 \sqrt{3}}{39} \cdot 130 \cdot \frac{1}{120}=\frac{200 \sqrt{3}}{9}
\]