Dowody Twierdzenia Pitagorasa
Twierdzenie Pitagorasa (wikipedia) ? twierdzenie geometrii euklidesowej dotyczące trójkątów prostokątnych, równoważne w istocie jest piątemu pewnikowi Euklidesa o prostych równoległych. W zachodnioeuropejskim kręgu kulturowym przypisuje się je żyjącemu w VI wieku p.n.e. greckiemu matematykowi i filozofowi Pitagorasowi, jednak odkrycia dokonali Babilończycy, którzy znali dodatkowo dwie prostsze metody, przy których błąd jest niewielki. Zapewne znali je przed Pitagorasem starożytni Egipcjanie. Prawdopodobnie jeszcze przed nim znano je w starożytnych Chinach i Indiach.
Twierdzenie Pitagorasa
W dowolnym trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej tego trójkąta.
a2 + b2 = c2
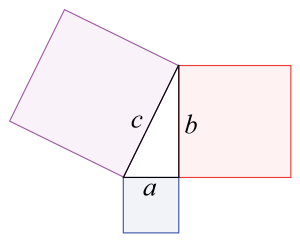
Geometrycznie oznacza to, że jeżeli na bokach trójkąta prostokątnego zbudujemy kwadraty, to suma pól kwadratów zbudowanych na przyprostokątnych tego trójkąta będzie równa polu kwadratu zbudowanego na przeciwprostokątnej.
Dowody twierdzenia Pitagorasa
Liczba różnych dowodów twierdzenia Pitagorasa jest bardzo duża ? Euklides w Elementach podaje ich osiem, kolejne pojawiały się na przestrzeni wieków i pojawiają aż po dni dzisiejsze. Opublikowano przynajmniej 118 geometrycznych dowodów twierdzenia Pitagorasa, a Friedrichs udowodnił, że jest ich nieskończenie wiele.
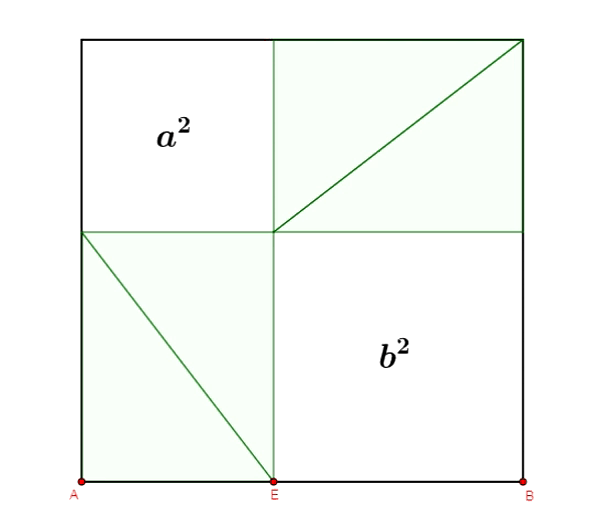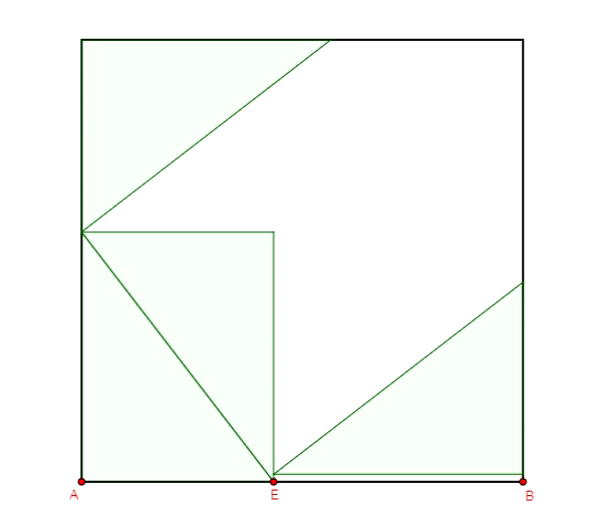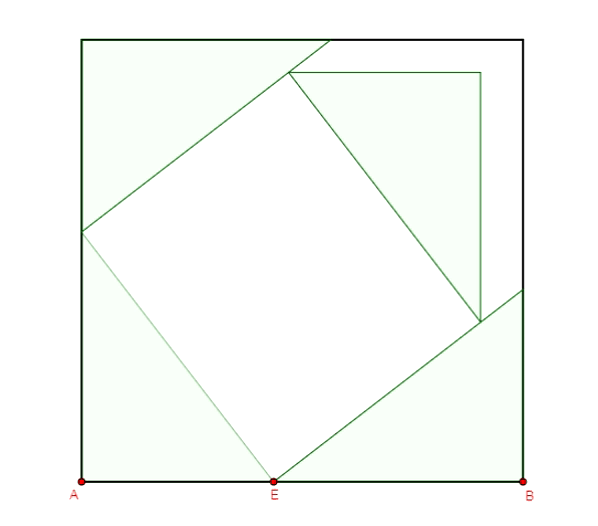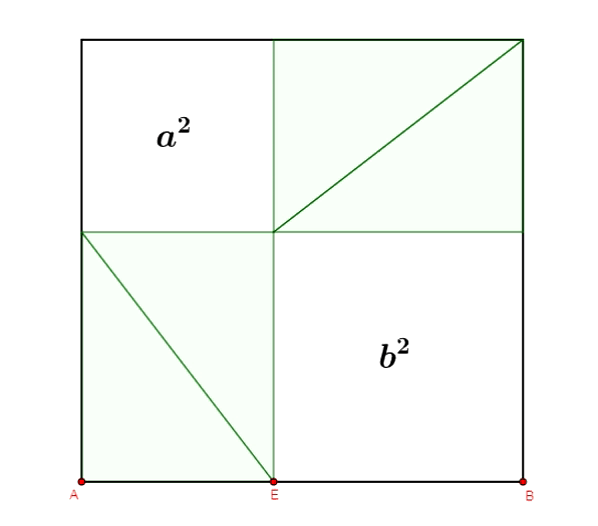
Zobaczmy kilka ilustracji dowodów twierdzenia Pitagorasa wykonanych w programie GeoGebra.
Twierdzenie Pitagorasa - dowód Annarizi z Arabii
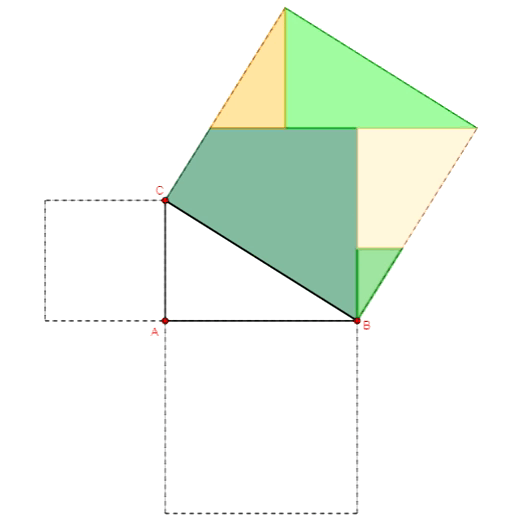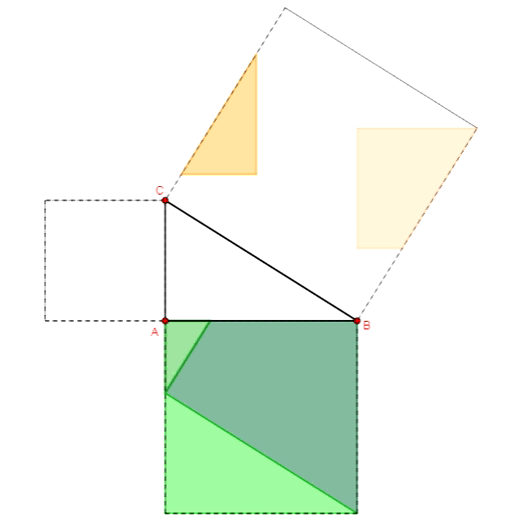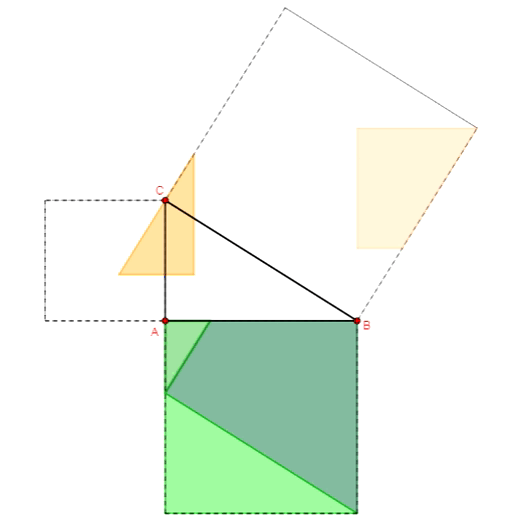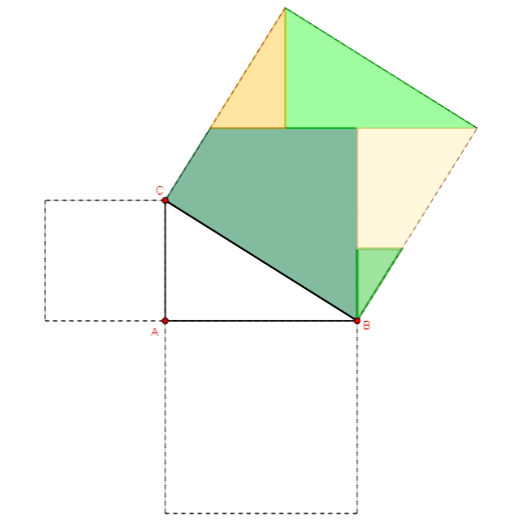
Twierdzenie Pitagorasa - dowód Bottchera
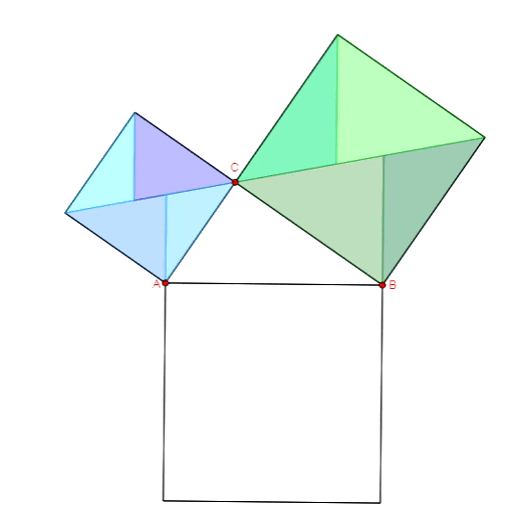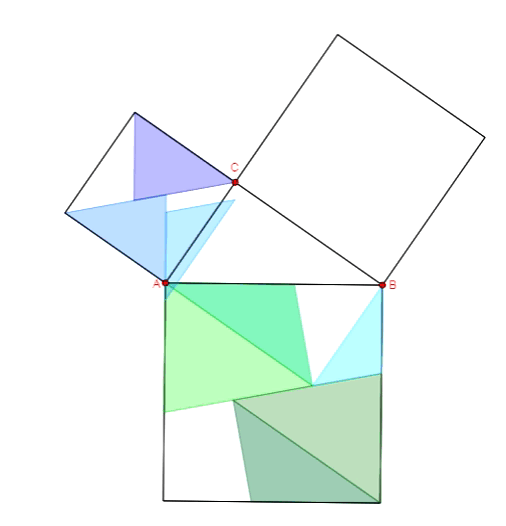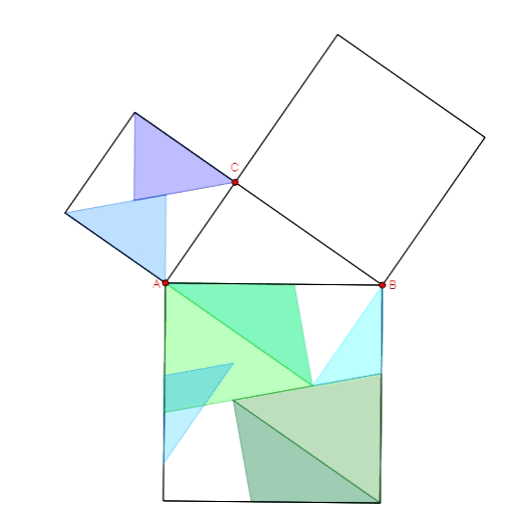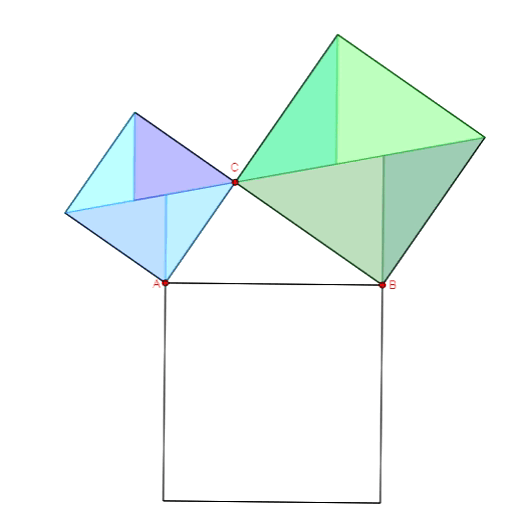
Twierdzenie Pitagorasa - dowód Dudeney'a

Twierdzenie Pitagorasa - dowód Henry'ego Perigala
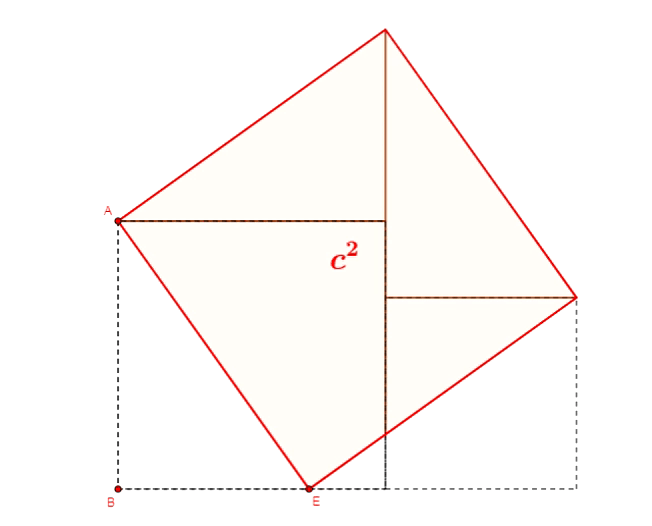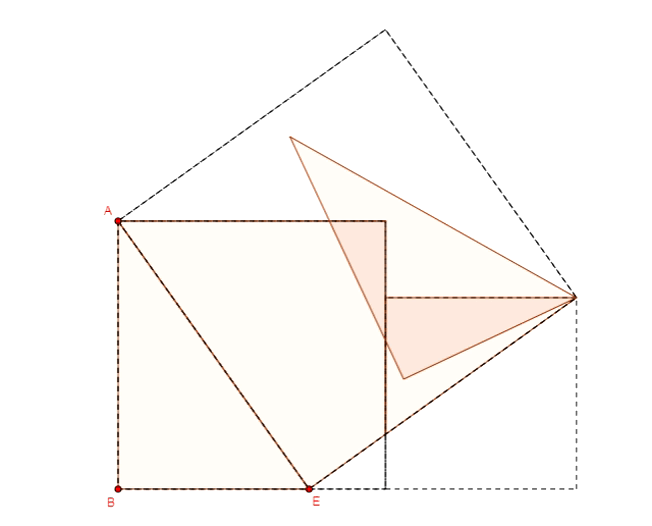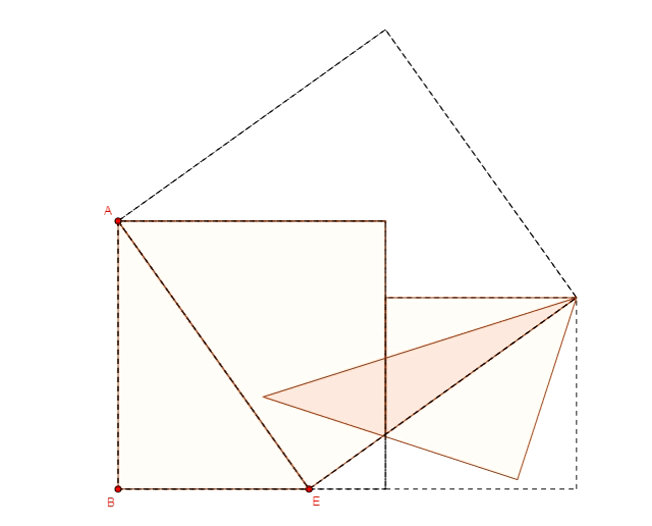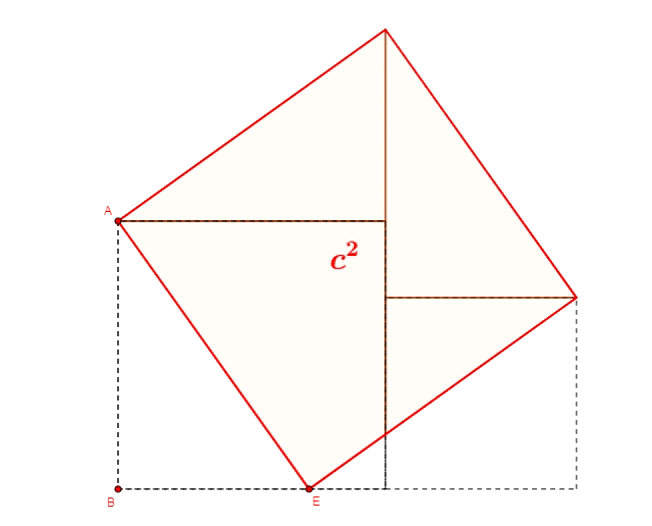
Twierdzenie Pitagorasa - dowód Jamesa Abrama Garfielda
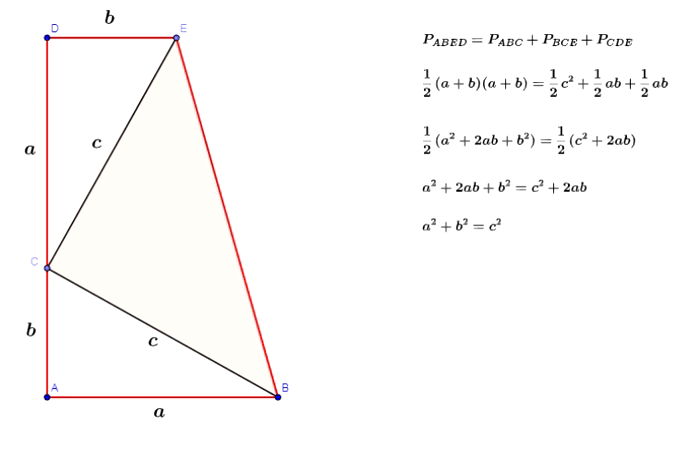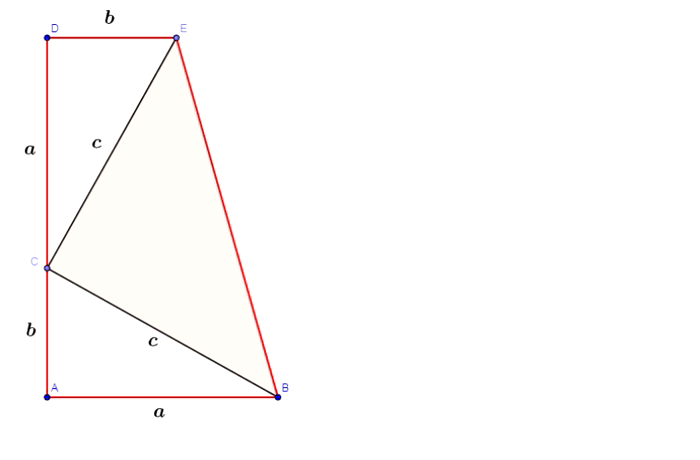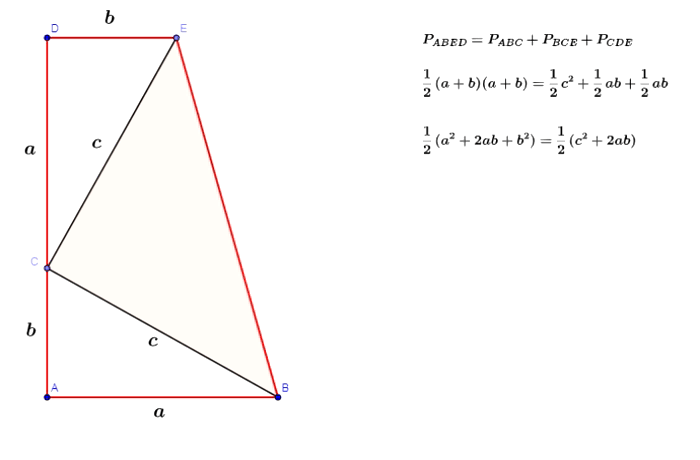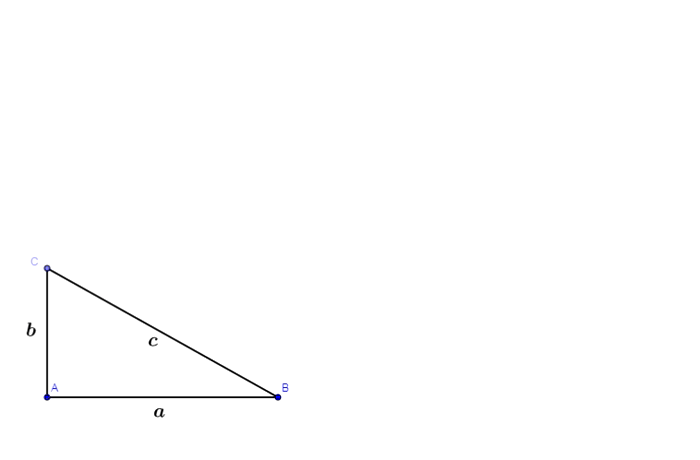
Twierdzenie Pitagorasa - dowód Leonarda da Vinci
Twierdzenie Pitagorasa - dowód Liu Hui
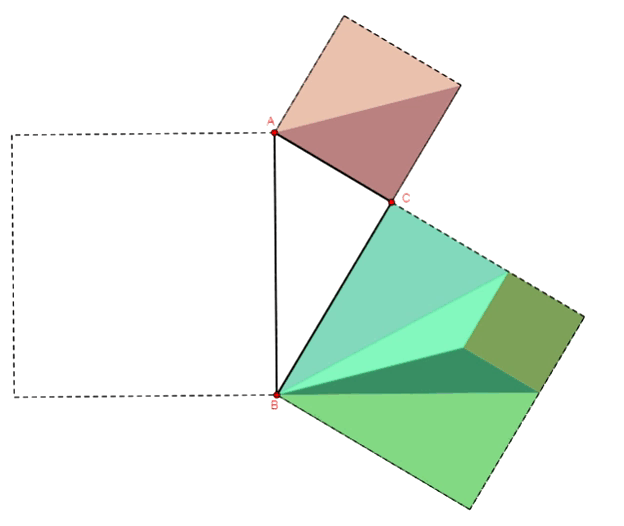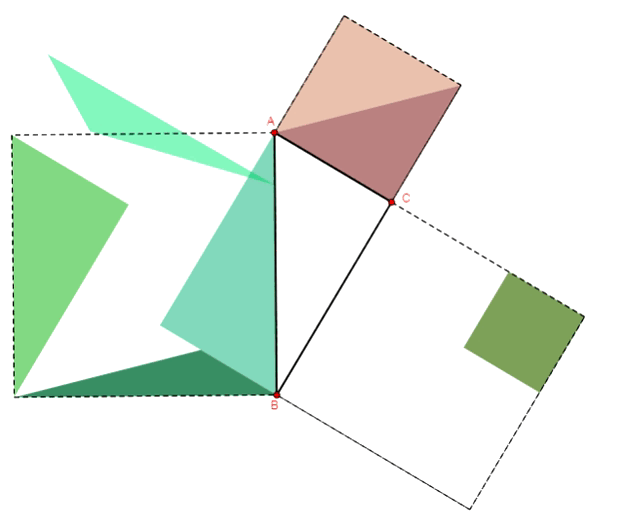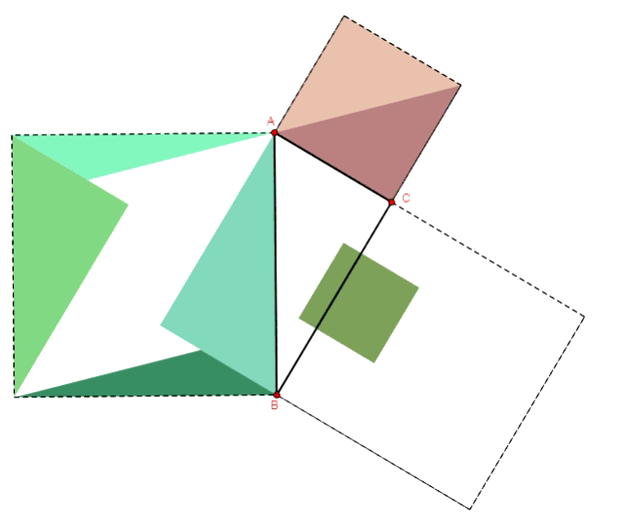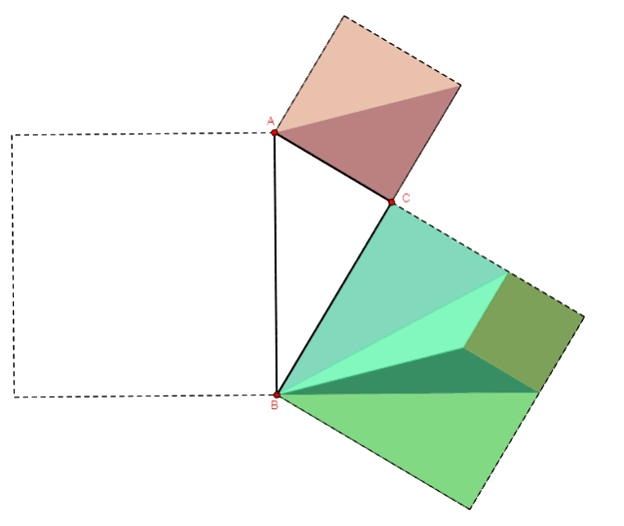
Twierdzenie Pitagorasa - dowód Euklidesa
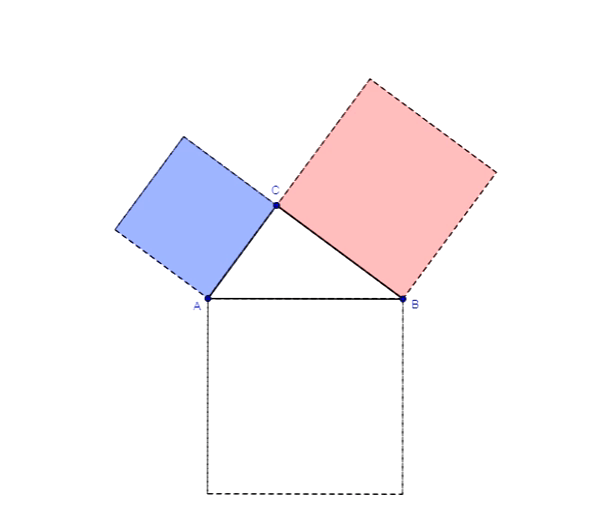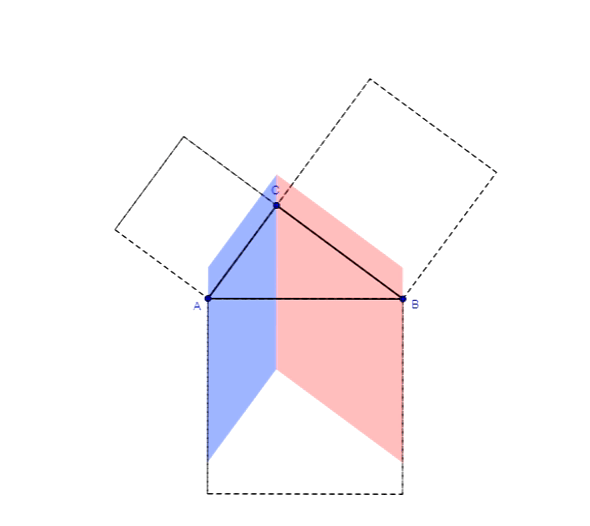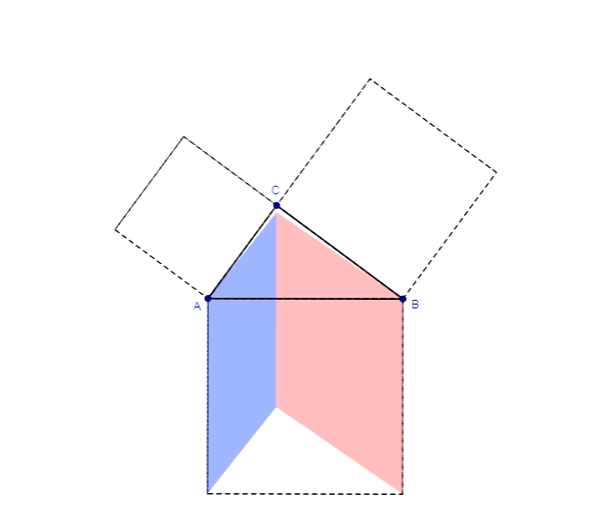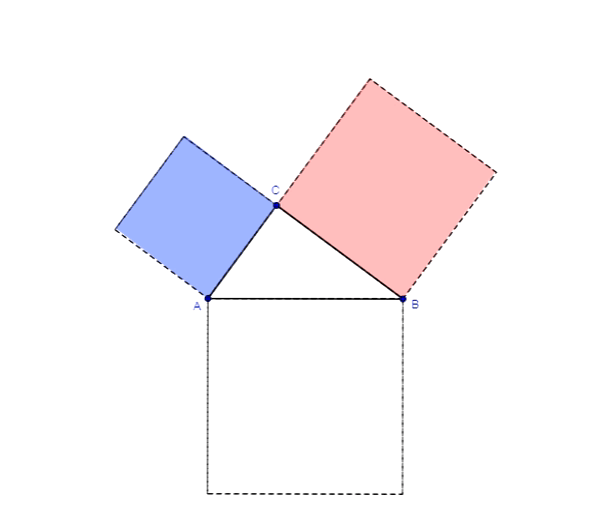
Twierdzenie Pitagorasa dowód z Chou Pei Suan Ching