Ruletka i matematyka

Matematyczne rozmaitości Odsłon: 1195

Czy wiesz, że ruletka została wymyślona przez matematyka?

Ale może od początku. Co to jest ruletka?

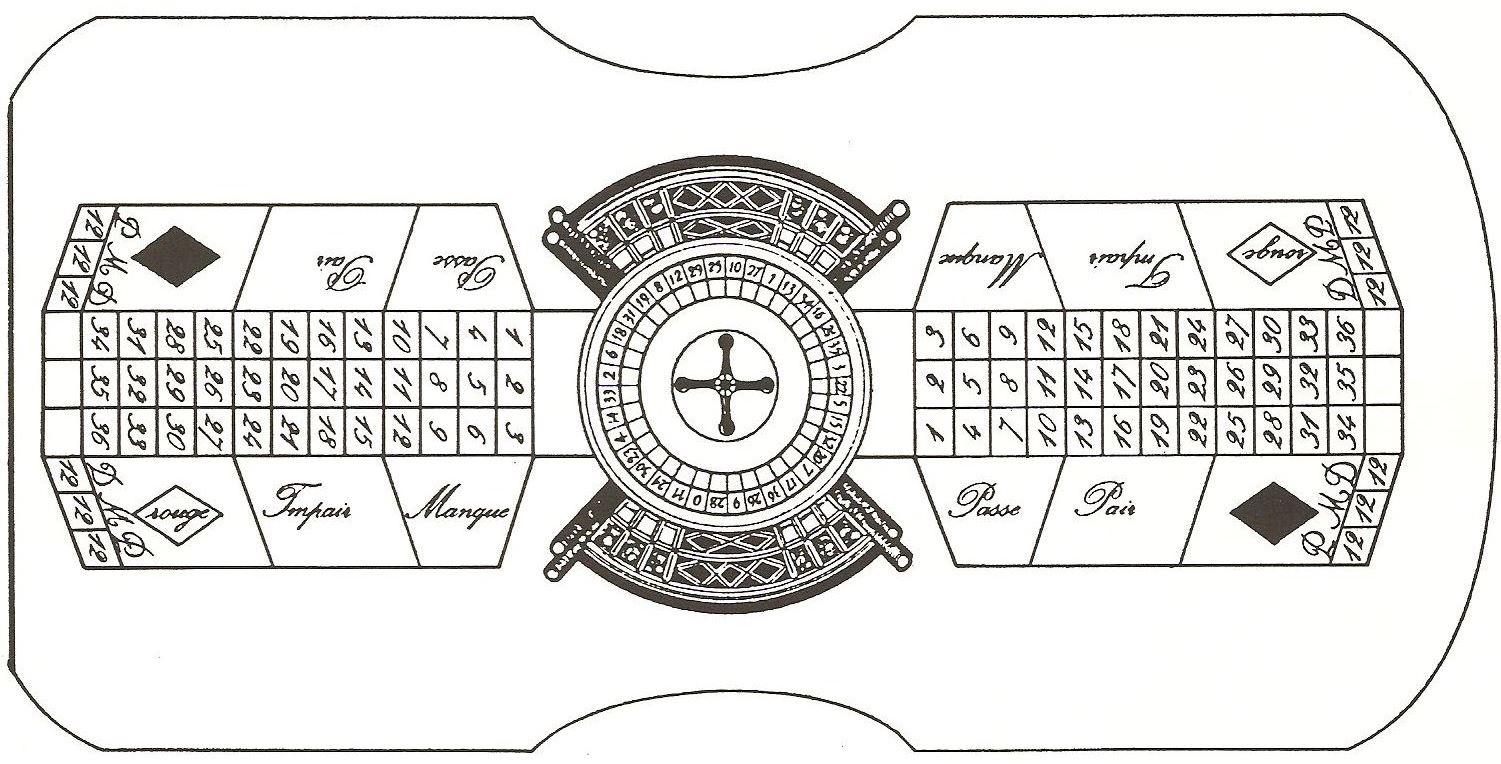
Ruletka – to pseudolosowa, często hazardowa gra, grana w większości kasyn. Są dwa podstawowe systemy ruletki: europejski i amerykański. Nazwa ruletka pochodzi od francuskiego słowa oznaczającego małe koło. W grze gracz może postawić zakład na pojedynczą liczbę, różne grupy liczb, kolor czerwony lub czarny, czy liczba jest parzysta czy nieparzysta, czy liczba jest wysoka (19–36) czy niska ( 1–18). Aby określić zwycięską liczbę, krupier kręci kołem w jednym kierunku, a następnie kręci kulką w przeciwnym kierunku wokół nachylonego okrągłego toru biegnącego wokół zewnętrznej krawędzi koła. Piłka w końcu traci pęd , przechodzi przez obszar deflektorów i opada na koło, wpadając do jednej z trzydziestu siedmiu (ruletka z jednym zerem, francuska lub europejska) lub trzydziestu ośmiu (ruletka z podwójnym zerem, w stylu amerykańskim) lub trzydzieści dziewięć (potrójne zero, „Sands Roulette”) kolorowe i ponumerowane kieszenie na kole. Wygrane są następnie wypłacane każdemu, kto postawił udany zakład. 

Trochę historii

W pierwotną wersję ruletki grali już starożytni Grecy, ale wielu historyków uważa, że ruletkę wymyślił w 1645 r. francuski uczony, fizyk, matematyk Blaise Pascal na bazie swoich matematycznych zainteresowań rachunkiem prawdopodobieństwa.

Blaise Pascal

ur. 19 czerwca 1623 w Clermont-Ferrand, zm. 19 sierpnia 1662 w Paryżu

Była to jednak dość prymitywna wersja gry i dopiero pierwsza forma ruletki została wymyślona we Francji w XVIII wieku. Mechanizm ruletki jest hybrydą koła do gier wynalezionego w 1720 roku i włoskiej gry Biribi. Prymitywna forma ruletki, znana jako 'EO' (Even/Odd - Parzyste/Nieparzyste), była grana w Anglii pod koniec XVIII wieku przy użyciu koła do gier podobnego do tego używanego w ruletce. 

XVIII-wieczne koło EO z graczami

Gra jest grana w swojej obecnej formie co najmniej od 1796 roku w Paryżu. Wczesny opis gry ruletka w jej obecnej formie znajduje się we francuskiej powieści "La Roulette, ou le Jour" Jacques'a Lablee, która opisuje koło ruletki w Palais Royal w Paryżu w 1796 roku. Opis zawiera kieszenie dla domu: "Dokładnie dwie przestrzenie są zarezerwowane dla banku, skąd czerpie on jedyną matematyczną przewagę". Następnie opisuje układ z "...dwoma polami do zakładów zawierającymi dwa numery banku, zero i podwójne zero". Książka została opublikowana w 1801 roku. Jeszcze wcześniejsza wzmianka o grze o tej nazwie została opublikowana w regulacjach dla Nowej Francji (Québec) w 1758 roku, które zakazywały gier w "kości, hoca, faro i ruletkę". 

XIX-wieczna rycina przedstawiająca francuską ruletkę

W 1842 Louis Blanc – francuski polityk i historyk wraz z bratem Francisem dołożyli 0 do ruletki Pascala, by zwiększyć szanse wygrania domu (kasyna). Założyli także pierwsze kasyno w Monako. Od tego czasu ruletkę niektórzy nazywają królową kasyn. Potem ruletkę sprowadzono do Stanów Zjednoczonych, gdzie dołożono pole z numerem 00.

Trochę matematyki

W ruletce w wersji eupropejskiej mamy liczby od 1 do 36 oraz 0  - czyli 37 pól (kieszeni) oraz w wersji amerykańskiej liczby 0d 1 do 36, 0 i 00 - czyli 38 pól (kieszeni).

Zatem

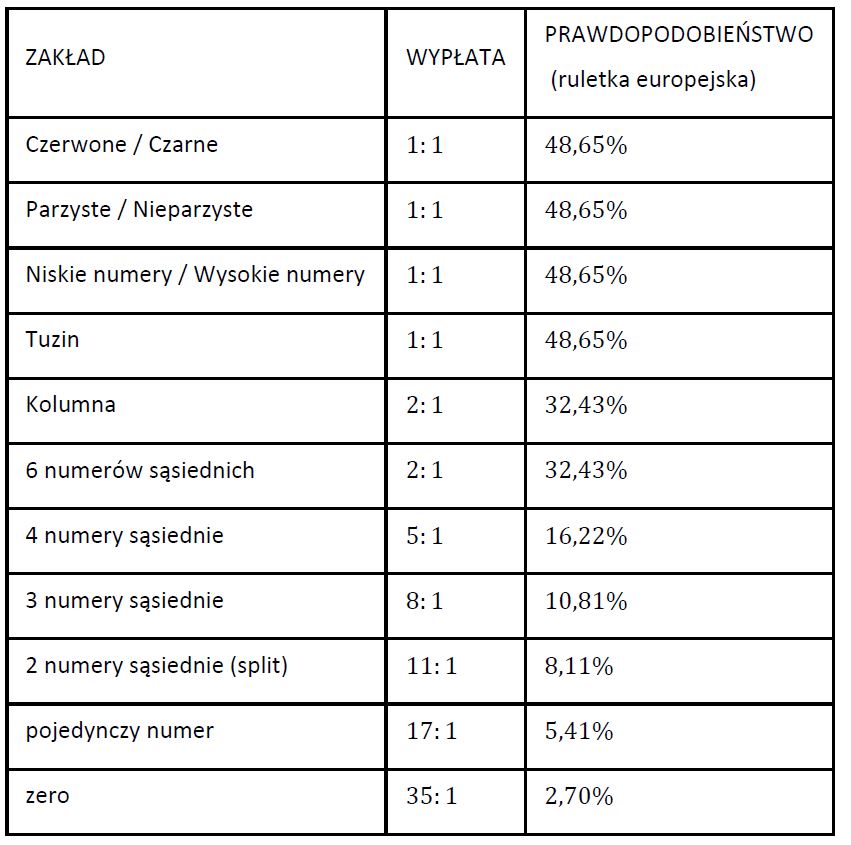
Szansa na prawidłowy wybór jednej liczby w grze w ruletkę wynosi 1:37. Innymi słowy, podczas gry w ruletkę francuską (jedno zero) szansa na wygraną wynosi 2,7%, a podczas gry w ruletkę amerykańską (dwa zera) 2,63%.

Przykłady innych zakładów w ruletce europejskiej:

Oczekiwaną wartość zakładu o wartości 1 dolara (z wyjątkiem specjalnego przypadku zakładów Top line) w przypadku ruletki amerykańskiej i europejskiej można obliczyć jako
\[
\text { expectedvalue (EX)}=\frac{1}{n}(36-n)=\frac{36}{n}-1,
\]
gdzie \(n\) jest liczbą kieszeni w kole.
Początkowy zakład jest zwracany oprócz wspomnianej wypłaty: można łatwo wykazać, że ta formuła wypłaty doprowadziłaby do zerowej oczekiwanej wartości zysku, gdyby było tylko 36 liczb (co oznacza, że kasyno osiągnęłoby próg rentowności). Posiadanie 37 lub więcej liczb daje kasynu przewagę. Mówiąc dokładniej:

1. W ruletce europejskiej jest 37 kieszeni (numery od 1 do 36 oraz jedno zero). Dlatego w przypadku tej wersji gry \(n=37\).
2. W ruletce amerykańskiej jest 38 kieszeni (numery od 1 do 36 , zero oraz podwójne zero). Dlatego w przypadku tej wersji gry \(n=38\).

Korzystając z podanej formuły, możemy obliczyć oczekiwaną wartość zakładu o wartości 1 dolara dla obu wersji ruletki:
Dla ruletki europejskiej:
\[
\text { EX }=\frac{36}{37}-1=-\frac{1}{37} \approx-0.027 .
\]
To oznacza, że oczekiwana strata na każdy postawiony dolar wynosi około 2.7 centów.
Dla ruletki amerykańskiej:
\[
\text { EX }=\frac{36}{38}-1=-\frac{1}{19} \approx-0.0526 .
\]
To oznacza, że oczekiwana strata na każdy postawiony dolar wynosi około 5.26 centów.
Przewaga kasyna wynika z obecności jednego lub dwóch zer na kole ruletki, które nie są uwzględniane w standardowych wypłatach dla graczy. W obu przypadkach, gdyby było dokładnie 36 kieszeni i wypłata była dokładnie taka sama jak liczba kieszeni, zakład byłby uczciwy i nie byłoby przewagi dla kasyna ani gracza. Jednak dodatkowe kieszenie (zero i/lub podwójne zero) zapewniają kasynu przewagę w dłuższej perspektywie.

Zatem matematyka to jedno, a szczęście to już co innego. 

Ciekawostka

Suma wszystkich liczb w ruletce daje 666, stąd często nazywa się ruletkę, jako „szatańska gra”.

Podsumowanie

Zrozumienie matematycznych podstaw gier hazardowych jest kluczowe dla każdego, kto myśli o grze, niezależnie od tego, czy jest to dla rozrywki, czy z poważniejszymi zamiarami. Oto kilka powodów, dla których warto znać stronę matematyczną:

1. Przewaga Kasyna: W większości gier kasynowych, kasyno ma matematyczną przewagę nad graczem. Oznacza to, że w dłuższej perspektywie, kasyno zawsze będzie w przewadze.

2. Świadome Decyzje: Jeśli rozumiesz prawdopodobieństwa i oczekiwane wartości, możesz podejmować bardziej świadome decyzje podczas gry, minimalizując potencjalne straty.

3. Unikanie Pułapek: Niektóre gry lub zakłady mają znacznie gorsze prawdopodobieństwo zwycięstwa dla gracza niż inne. Znając matematykę, możesz unikać tych "pułapek".

4. Rozrywka vs Realność: Dla wielu ludzi gry hazardowe są formą rozrywki. Jednak rozumienie matematyki pozwala zobaczyć realną cenę tej rozrywki, co może pomóc unikać hazardu.

5. Zapobieganie Uzależnieniom: Wiedza o tym, jakie są szanse i jak działają gry, może pomóc w uniknięciu złudzeń o "pewnych metodach wygrywania" i tym samym w zapobieganiu potencjalnemu uzależnieniu.

To tylko kilka powodów, ale ogólnie rzecz biorąc, rozumienie matematyki gier daje graczowi lepszą perspektywę i pozwala podejmować bardziej świadome decyzje. Mimo to zawsze warto pamiętać, że hazard nie powinien być traktowany jako sposób na zarobienie pieniędzy. Jeśli ktoś czuje, że może mieć problem z hazardem, powinien poszukać specjalistycznej pomocy w poradniach uzależnień.