
Pszczoły to niezwykle fascynujące stworzenia, które potrafią wykazywać pewne zdolności matematyczne i architektoniczne. Niezmiernie ciekawy tryb życia, jaki prowadzą pszczoły, już z dawien dawna zwrócił uwagę ludzi nauki. Pszczoły miodne (Apis mellifera) są doskonałymi inżynierami, tworząc skomplikowane struktury w postaci plastra z sześciokątnymi komórkami, znane jako plastry miodu. Wielu z nas widziało taki plaster miodu na żywo, a być może niektórzy mieli przyjemność spróbować miodu z takiego plastra. Gdy weźmiemy taki plaster do ręki, natychmiast poczujemy, że jest dość ciężki jak na swoje rozmiary – wiadomo, miód ma swoją wagę. Ale to nie wszystko. Okazuje się bowiem, że przy tym ciężarze, plaster ten wytrzymuje dosyć duże naprężenia. Co wpływa na ten ciężar? Na pewno wspomniany wcześniej miód, ale również jego ilość. Przecież miód wypełnia prawie całą przestrzeń takiego plastra, nie ma w nim niewykorzystanych obszarów. Pszczoły unikają nieużytków w swoich ulach. Wynika to z wielu powodów. Na pewno jednym z powodów jest mała objętość ula, ale przecież niektóre pszczoły tworzą swoje gniazda poza ulem, a drugim powodem jest niezwykła zdolność architektoniczna pszczół. I na tym właśnie skupimy się w dalszej części artykułu. Zaskakujące jest to, że te komórki są optymalne pod względem minimalizacji zużycia wosku i zachowania stabilności struktury plastra. Pszczoły muszą dokładnie „obliczyć” odpowiednie kąty i długości boków każdej komórki, aby cała struktura była trwała i efektywna.
Przyjrzyjmy się bliżej instynktowi matematycznemu pszczół. Buduje ona tak, jak gdyby posiadała wysoką sprawność w stosowaniu wiedzy ścisłej. Chodzi tu m.in. o analizę matematyczną i teorię maximum i minimum. Wydaje się wręcz, że pszczoły "posiadają wiedzę" o figurach izoperymetrycznych, czyli jak znaleźć geometryczną figurę płaską o największym polu przy zadanym obwodzie. Pszczoła "stosuje" tą teorię w praktyce, gdy tymczasem człowiek dla odkrycia zależności w drobnej komórce musi wykorzystać wielowiekowy dorobek matematyczny. Pierwsza wzmianka o geometrycznych zdolnościach pszczół pochodzi z 36 r. p.n.e. od Marka Terencjusza Warrona, ale często przypisywana jest Pappusowi z Aleksandrii (ok. 290 - ok. 350), który rozpoczął badania nad zasadą budowy pszczelich komórek i opisał je za pomocą liczb. W XVI wieku wielu ciekawych spostrzeżeń dokonał Jan Brożek. Stworzył tzw. hipotezę plastra miodu, która stwierdza, że regularna sześciokątna siatka lub plaster miodu ma najmniejszy całkowity obwód z dowolnego podziału płaszczyzny na obszary o równej powierzchni. Przypuszczenie to zostało udowodnione w 1999 roku przez matematyka Thomasa C. Halesa. W XVIII wieku do problemem komórek pszczelich zajmowali się Moraldi, Réaumur, Koenig i Maclaurin, który dokonał dokładnych obliczeń matematycznych budowy komórki pszczelnej.
Trochę matematyki
Postaram się to wyjaśnić możliwie prosto – zgodnie z tym jak powiedział Albert Einstein: „Wszystko należy robić tak prosto jak to możliwe, ale nie prościej”.
Plastry pszczele są zabudowane obustronnie regularnymi sześciokątnymi komórkami, ułożonymi w rzędach, ukośnie odchylonymi ku górze, tak by nie dochodziło do wyciekania z nich niedojrzałego płynnego nakropu. Ustawione tak pod kątem 9-14° w stosunku do poziomu sześciokątne komórki zamyka dno, utworzone z trzech rombów stykających się pod kątem 107°. Trzy romby stanowią jednocześnie dno trzech komórek znajdujących się po drugiej stronie plastra. Każda ze ścianek bocznych jednej komórki stanowi jednocześnie ściankę sąsiedniej przylegającej do niej komórki. Pomiędzy ściankami bocznymi zachowany jest kąt 120°. Trochę to złożone, ale poniższe rysunki powinny zrozumienie.
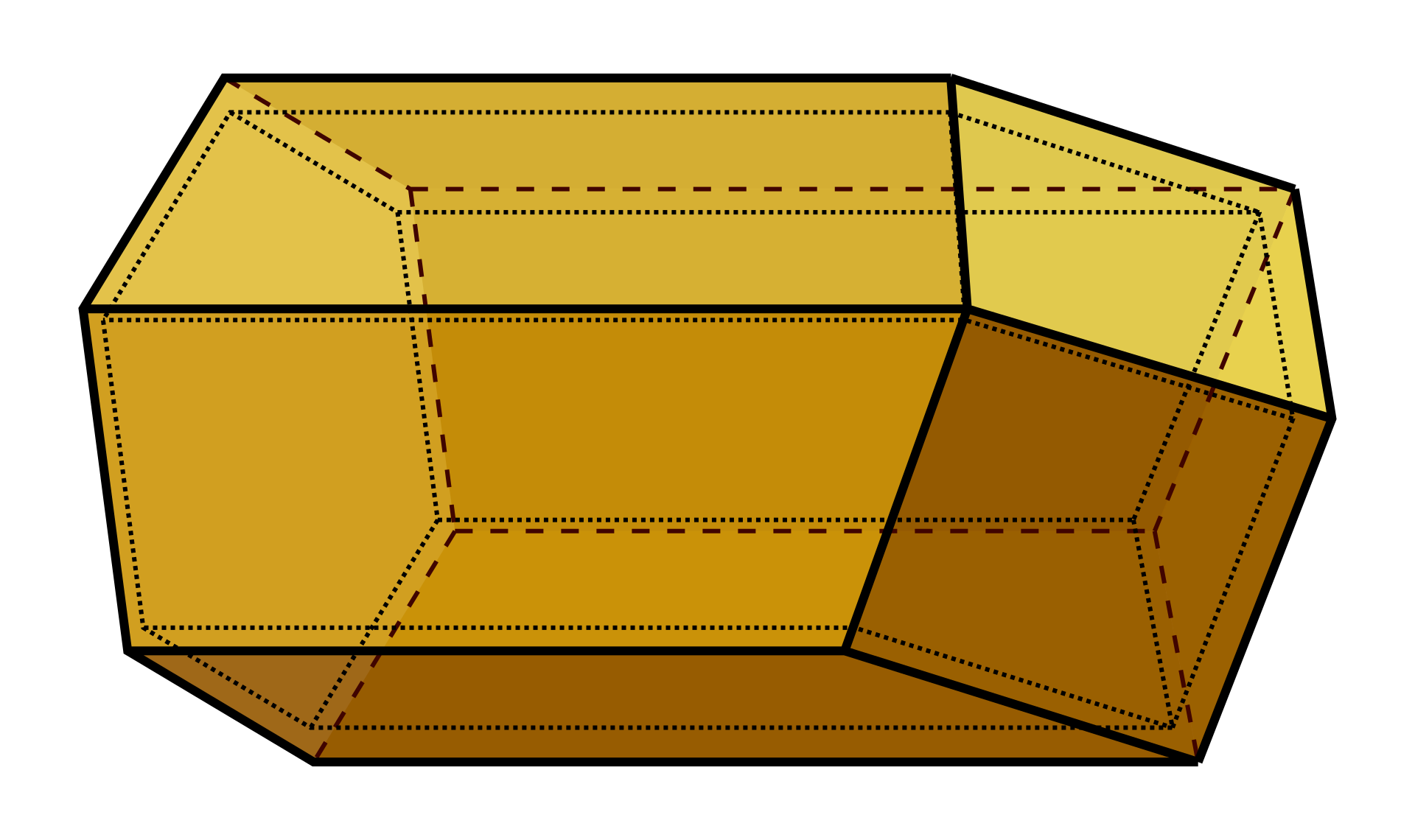 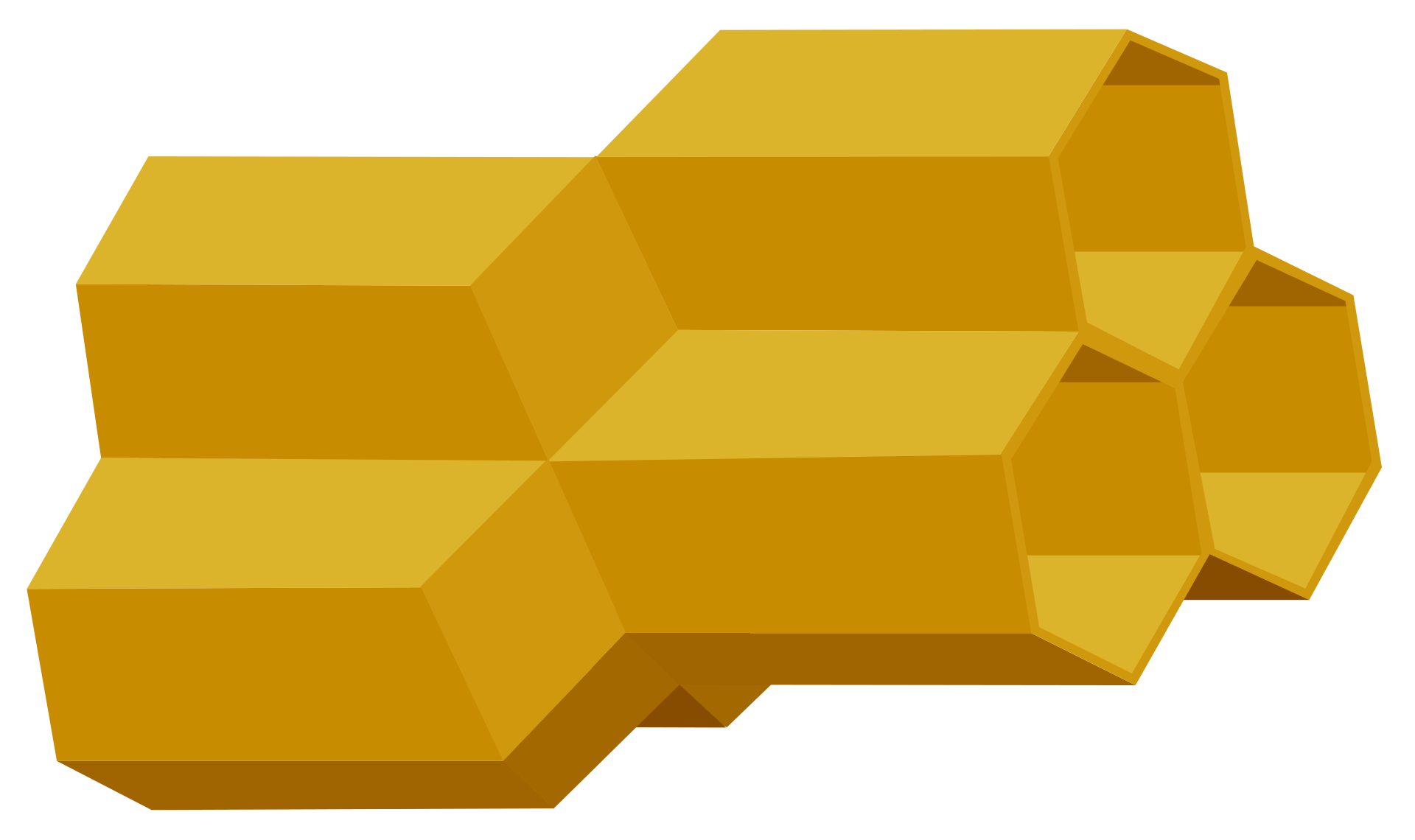 |
Grubość ścianek komórek pszczelich wynosi 0,073±0,002 mm a dna komórek od 0,110-0,142 mm. Miejsca połączeń poszczególnych płaszczyzn są nieco pogrubione podobnie jak zewnętrzne krawędzie ścian sześciokątnych komórek. Pogrubione krawędzie wzmacniają całą konstrukcję a jednocześnie nadają komórkom zaokrąglony kształt.
A teraz podejdźmy jeszcze bardziej szczegółowo - tak jak na lekcji matematyki :-) Takie oto podejście zaprezentował H.Niemirski w swojej książce W świecie matematycznej wyobraźni:
Przyjmijmy oznaczenia jak na poższym rysunku, przedstawiającym graniastosłup prosty, którego podstawą jest sześciokąt foremny.
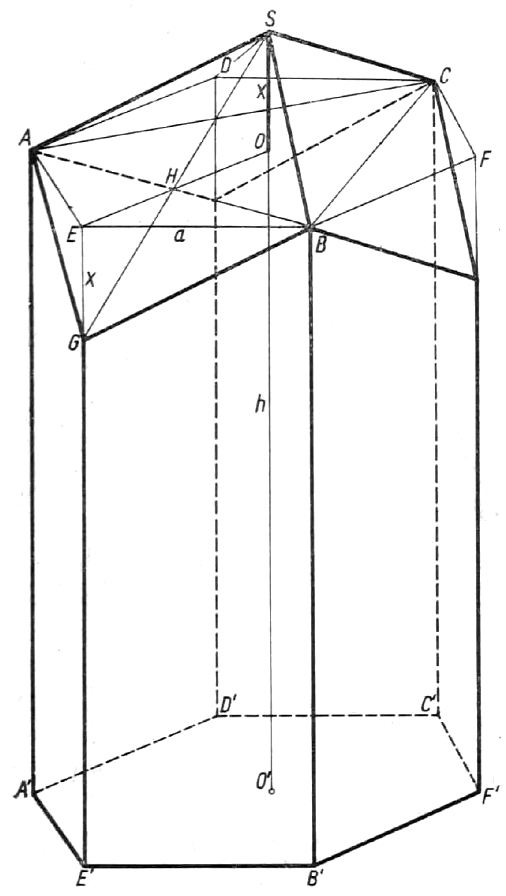
Połączmy w górnej podstawie parami wierzchołki: \(A\) z \(B\), \(B\) z \(C\), \(C\) z \(A\). Wydzielimy w ten sposób trójkąt \(A B C\). Przedłużmy wysokość \(O^{\prime} O\) bryły do na razie dowolnego - punktu \(S\), a następnie poprowadźmy płaszczyzny przez ten punkt i boki otrzymanego trójkąta. Powstaną trzy jednakowe romby (jednym z nich jest \(A S B G\) ), odcinające trzy naroża graniastosłupa z wierzchołkami \(E, F, D\). Naroża te mają postać ostrosłupów trójkątnych. Jeżeli obrócimy je wokół osi \(A B, B C, C A\) w ten sposób, aby ich ściany \(A E B, F B C, D A C\) znalazły się na płaszczyźnie górnej podstawy graniastosłupa, a więc o \(180^{\circ}\), to wierzcholki \(E, F, D\) spotkają się w punkcie \(O\), a trzy obrócone naroża utworzą nowy ostrosłup \(S-A B C\), przylegający do ścian naszych rombów. W efekcie przeprowadzonej konstrukcji otrzymujemy nową bryłę, posiadającą kształt komórki pszczelnej, co pokazuje poniższy rysunek.
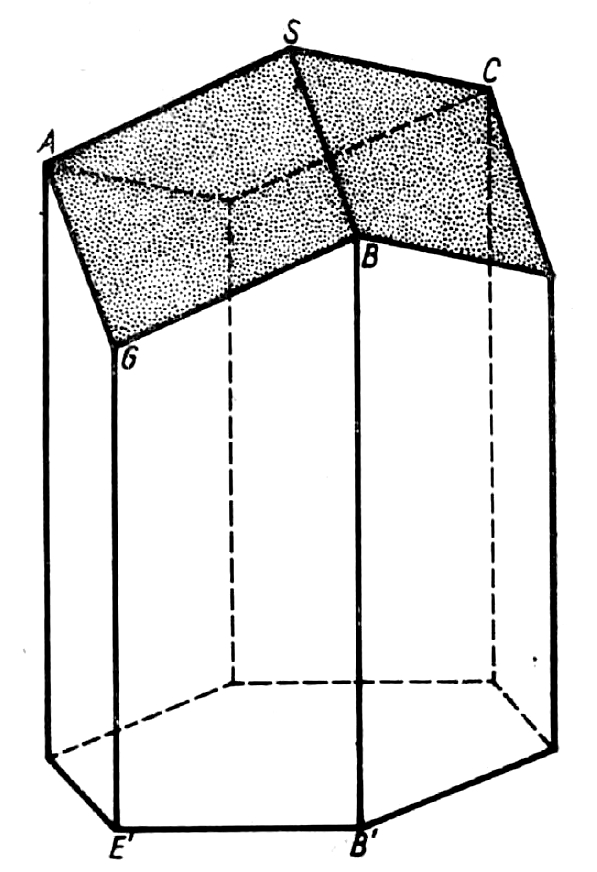
Widać na nim już wyraźnie kształty trzech rombów typu \(A S B G\) oraz sześciu ścian bocznych typu \(G B B^{\prime} E^{\prime}\) w postaci trapezów. Zaciekawia już sama konstrukcja, która od sześciokątnego graniastosłupa doprowadziła do bryły o dość zastanawiających kształtach. Narzucają się wyraźnie dwa wnioski:
1. Odcięte i obrócone naroża zmieniły tylko postać graniastosłupa. Otrzymana bryła musi zatem mieć tę samą co graniastosłup objętość.
2. Zmieniona została powierzchnia bryły i jest mianowicie mniejsza od powierzchni wyjściowej. Znikną np. przy wierzchołku \(E\) trzy trójkąty, a ich miejsce zajmie romb \(S A G B\).
A teraz trochę obliczeń.
Czy jest jakaś celowość w tym, że zamiast zwykłego graniastosłupa pszczoła wybrała bardziej skomplikowaną formę? Obliczmy powierzchnię komórki, wprowadzając oznaczenia: \(O S=x, O O^{\prime}=h, E B=a\).
Pole rombu \(S A G B\) wynosi
(1) \(P_r=\frac{A B \cdot S G}{2}\)
Z trójkąta \(E H B\), w którym \(E H=\frac{a}{2}\), otrzymamy:
skąd
\((H B)^2=(E B)^2-(E H)^2\)
\(\begin{gathered}(H B)^2=a^2-\left(\frac{a}{2}\right)^2 ;(H B)^2=a^2-\frac{a^2}{4} \\(H B)^2=\frac{3 a^2}{4} ; H B=\frac{a \sqrt{ } 3}{2}\end{gathered}\)
i wreszcie, ponieważ \(A H=H B\)
\(A B=a \sqrt{3}\)
Długość \(G S=2 H S\) obliczymy z trójkąta \(O H S\) :
\((H S)^2=(H O)^2+(O S)^2\)
Kładąc tu \(O S=x\) oraz \(H O=\frac{a}{2}\) otrzymamy:
\((H S)^2=\frac{a^2}{4}+x^2\)
skąd \(H S=\sqrt{\frac{a^2}{4}+x^2}\) oraz \(G S=2 \sqrt{\frac{a^2}{4}+x^2}\)
Otrzymane wartości przekątnych rombu \(A B\) i \(G S\) możemy wstawić do związku (1). Będzie:
(2) \(P_x=a \sqrt{3} \cdot \sqrt{\frac{a^2}{4}+x^2}\)
Pole trapezu \(G B B^{\prime} E^{\prime}\) wyprowadzimy wg wzoru
(3) \(P_t=\frac{B B^{\prime}+G E^{\prime}}{2} \cdot E^{\prime} B^{\prime}\)
Podstawiając \(B B^{\prime}=h, G E^{\prime}=h-x, E^{\prime} B^{\prime}=a\), otrzymamy ze związku (3):
(4) \(P_{\mathrm{t}}=\frac{a}{2}(2 h-x)\)
Pole całej komórki złożyć już łatwo z trzech pól rombów (2) i sześciu pól trapezów (4). W wyniku otrzymamy:
(5) \(P=3 a \sqrt{3} \cdot \sqrt{\frac{a^2}{4}+x^2}+3 a(2 h-x)\)
W związku (5) występuje niewiadoma \(x\), określająca położenie wierzchołka \(S\) komórki. Otóż wartość \(x\) pszczoła dobiera w taki sposób, aby powierzchnia bryły była możliwie najmniejsza. Dzieląc obie strony wzoru (5) przez \(3 a\) i wprowadzając oznaczenie \(\frac{P}{3 a}=y\) otrzymamy:
\(\sqrt{3} \cdot \sqrt{\frac{a^2}{4}+x^2}+2 h-x=y\)
skąd
\(\begin{aligned}& \sqrt{3} \cdot \sqrt{\frac{a^2}{4}+x^2}+2 h-x=y \\& \sqrt{3} \cdot \sqrt{\frac{a^2}{4}+x^2}=x+y-2 h\end{aligned}\)
Po podniesieniu obu stron równania do kwadratu i po znanych przekształceniach otrzymujemy:
(6) \(\begin{gathered}8 x^2-8(y-2 h) x+\left[3 a^2-4(y-2 h)^2\right]=0 \\x=\frac{1}{2}(y-2 h) \pm \frac{1}{4} \sqrt{6\left[2(y-2 h)^2-a^2\right]}\end{gathered}\)
Niewiadoma \(x\) musi mieć wartość rzeczywistą. Stąd wyrażenie:
\(2(y-2 h)^2-a^2 \geqslant 0\)
Po krótkich przekształceniach otrzymamy:
\(y \geqslant \frac{a}{\sqrt{2}}+2 h\)
Najmniejszą spośród możliwych w naszym zagadnieniu będzie wartość \(y=\frac{a}{\sqrt{2}}+2 h\). Dla obliczenia wartości \(x\) podstawiamy otrzymane wyrażenie na \(y\) do związku (6). Otrzymamy:
(7) \(x=\frac{a \sqrt{2}}{4}\)
a pole powierzchni ze wzoru (5) przyjmie ostateczną postać
(8) \(P=6 a h+\frac{3 a^2 \sqrt{2}}{2}\)
Obliczenie pola powierzchni graniastosłupa jest proste. Bez szczegółowych wyprowadzeń napiszemy gotową odpowiedź:
(9) \(P_g=6 a h+\frac{3 a^2 \sqrt{3}}{2}\)
Aby zdać sobie sprawę z różnicy pól powierzchni obu brył, należy znaleźć różnicę wartości (8) i (9). Otrzymamy bardzo interesujący wynik:
\(P_{\mathrm{g}}-P=\frac{3 a^2}{2}(\sqrt{3}-\sqrt{2})\)
Ale \(\sqrt{3}=1,73205, \sqrt{2}=1,41421 \cdot \sqrt{3}-\sqrt{2}=0,32\). Wobec tego
\(P_g-P=\frac{a^2}{2}\)
Tak przedstawia się oszczędność pszczoły w budowaniu komórek. Wymierzono szerokość ścianki; wynosi ona \(a=2,71 \mathrm{~mm}\). Różnica \(\frac{a^2}{2}\) ma więc wartość \(3,7 \mathrm{~mm}^2\). Jest to znaczna oszczędność, jeżeli wziąć pod uwagę ogromną ilość komórek znajdujących się w plastrze miodu.
Budwa przestrzennego modelu pszczelej komórki
Powróćmy do rysunku naszego graniastosłupa, aby wziąć jeszcze pod uwagę romb \(A S B G\), a w nim trójkąt prostokątny \(AHS\). Oznaczmy kąt \(H A S\) przez \(\frac{8}{2}\). Na podstawie znanych już związków mamy
\(\frac{S H}{A H}=\frac{\frac{a \sqrt{6}}{4}}{\frac{a \sqrt{3}}{2}}\)
Po uproszczeniach otrzymamy
\(\frac{S H}{A H}=\operatorname{tg} \frac{\delta}{2}=\frac{\sqrt{2}}{2} ; \quad \operatorname{tg} \frac{\delta}{2}=0,7071 ; \quad \frac{\delta}{2}=54^{\circ} 44^{\prime}\)
i ostatecznie
\(\delta=109^{\circ} 28^{\prime}\)
Jest to wartość, odpowiadająca z bardzo dużym przybliżeniem wartości otrzymywanej przez bezpośrednie pomiary rombów w komórkach. \(\mathrm{Np}\). S. Koenig otrzymał z pomiarów \(\delta=109^{\circ} 26^{\prime}\).
W celu wykreślenia rombu możemy użyć znalezionego kąta \(\delta\). Inna droga prowadzi przez narysowanie przekątnych i zbudowanie na nich rombu. Potrzebne konstrukcje znajdziemy w rozdz. XI w opisie szeregu pożytecznych szablonów.
Rrozpatrzmy jeszcze trójkąty \(H S O\) i \(H E G\); są one równe i wobec tego odcinek \(E G=x\) i zgodnie z dokonanymi obliczeniami \(\operatorname{mamy} E G=\frac{a \sqrt{2}}{4}\)
Obecnie zbierzmy elementy, potrzebne do wykreślenia siatki komórki pszczelnej. Przyjmując do konstrukcji siatki przykładowo bok komórki \(a=40 \mathrm{~mm}\), a głębokość komórki około 3,5 razy większą, możemy z dostatecznym przybliżeniem ustalić zespół danych;
\(a=40 ; \quad A A^{\prime}=120 ; \quad E G=10 \sqrt{2} ; \quad \delta=109^{\circ} 28^{\prime}\)
Elementy te wystarczą w zupełności do skonstruowania siatki komórki pszczelej.
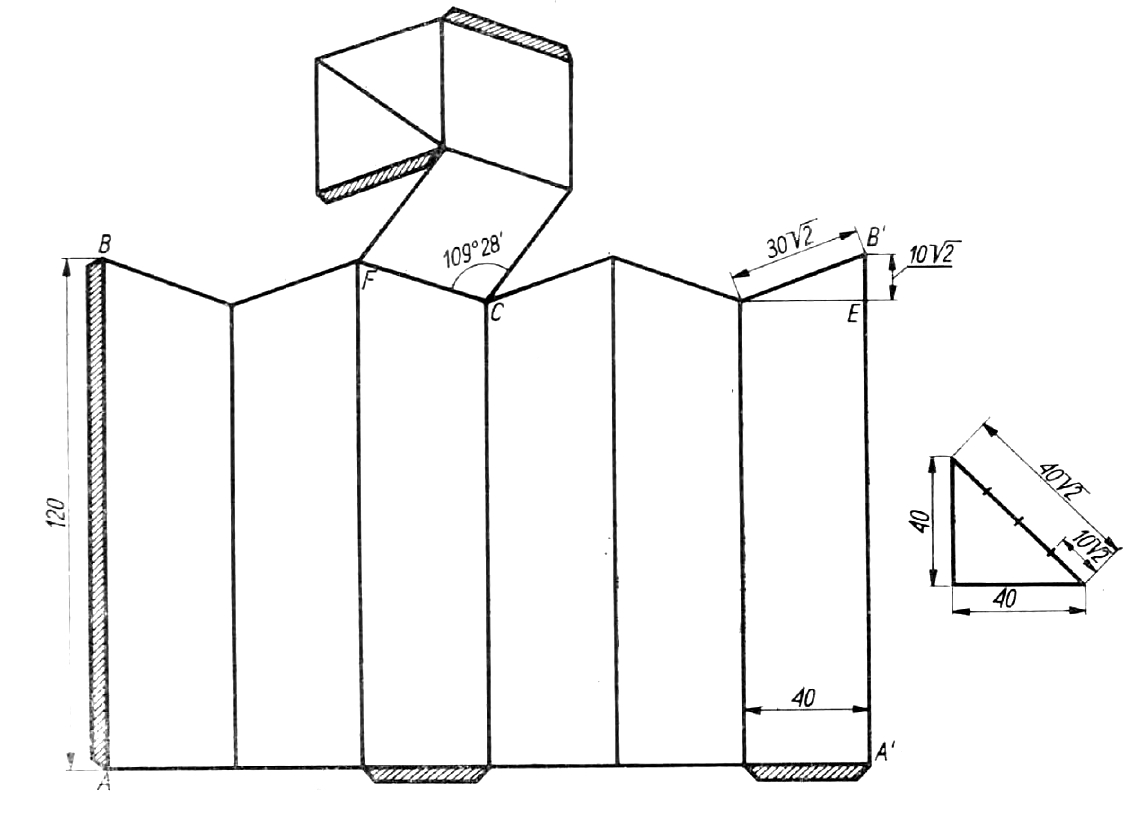
Powyższy rysunek przedstawia siatkę komórki pszczelnej o wymiarach, przyjętych wyżej przykładowo, którą możemy ustawić znanym już sposobem w okładkach. Elementy siatki kreślimy w następującej kolejności:
1. Kreślimy prostokąt \(A B A^{\prime} B^{\prime}\) złożony \(\mathrm{z}\) sześciu jednakowych prostokątów o wymiarach \(40 \mathrm{~mm} \times 120 \mathrm{~mm}\).
2. \(\mathrm{Na}\) boku \(A^{\prime} B^{\prime}\) ustalamy drogą prostej konstrukcji (patrz trójkąt prostokątny obok siatki) odcinek \(E B^r=10 \sqrt{2} \mathrm{~mm}\).
3. Z punktu \(E\) kreślimy prostą równoległą do \(A A^{\prime}\), uzyskując punkty jej przecięcia z bokami kolejnych prostokątów. Punkty te pozwolą otrzymać widoczną na siatce linię lamaną, złożoną z odcinków, z których każdy ma długość \(30 \sqrt{2} \mathrm{~mm}\).
4. Przy boku FC budujemy trzy romby o kącie rozwartym \(\delta=109^{\circ} 28^{\prime}\)
5. Po przeciągnięciu nici sklejamy siatkę i ustawiamy w okładkach w ten sam sposób, jak graniastosłup sześciokątny.
Model komórki pszczelnej możemy uzyskać również, konstruując siatkę samozwartą bez użycia kleju, jak na poniższym rysunku.
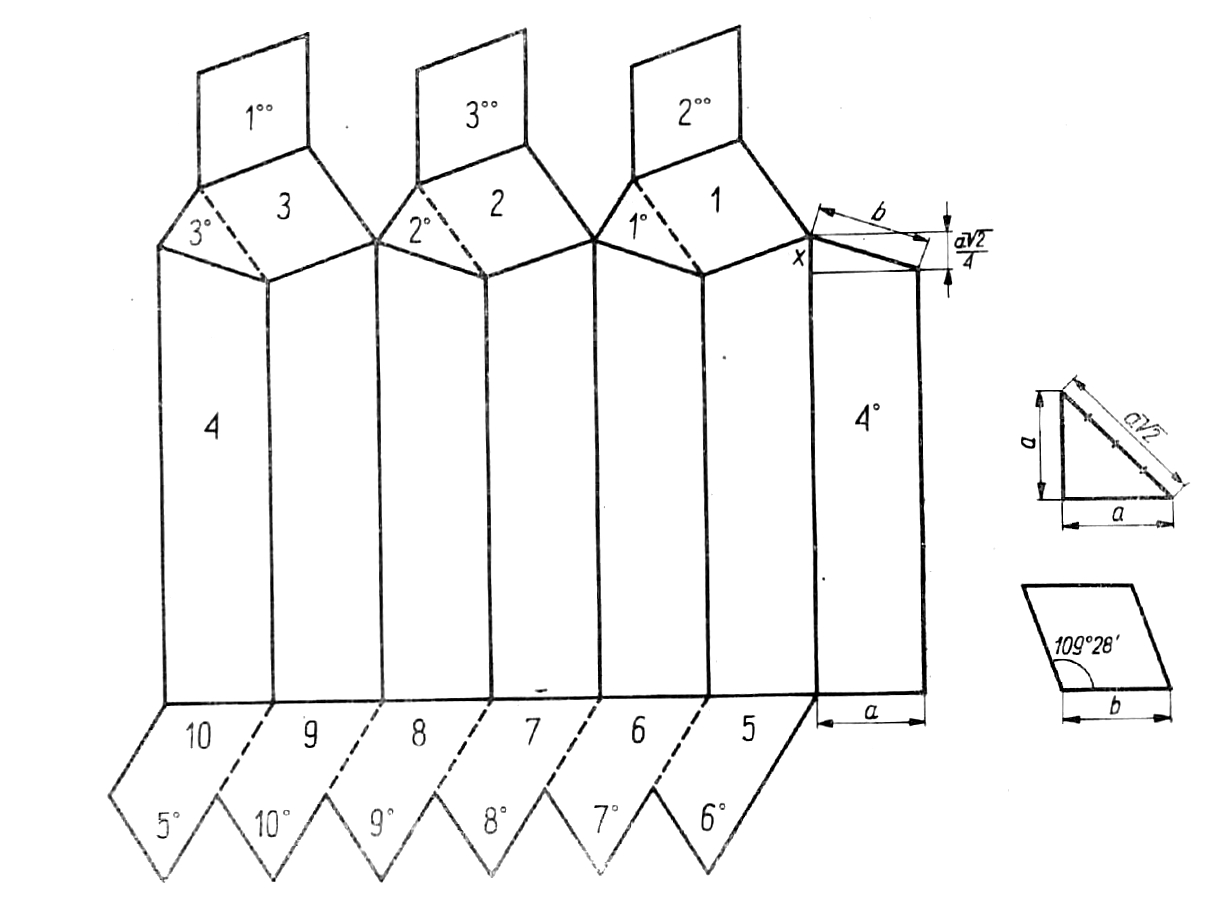
Wymiary na rysunku podane są dla dowolnie przyjętej długości boku \(a\); wykończenie dołu siatki (dna bryły) - jak w graniastosłupie sześciokątnym. Odcinki rysowane linią przerywaną należy przeciąć. Siatkę składamy w trwały model, splatając ścianki według poznanych już zasad. Potrzebne konstrukcje opisane są w następnym rozdziale książki.
Zapraszam do wykonania takiego modelu, jak również do poznania wielu innych interesujących rzeczy o pszczołach.
Odkrycia te są fascynujące i świadczą o tym, że nawet tak niewielkie stworzenia jak pszczoły potrafią wykazać zdolności matematyczne i architektoniczne. Jednakże, ważne jest, aby podkreślić, że wiedza pszczoły na ten temat jest wrodzona i nie oznacza, że świadomie rozumieją matematykę w taki sposób, jak my ludzie.
-------------------------------------------------------------
Bibliografia:
1. wikipedia.org
2. pasieka24.pl
3. H.Niemirski, W świecie matematycznej wyobraźni, PWSZ, 1963.

