Suwak logarytmiczny
czyli
genialny analogowy kalkulator

John Napier Joost Bürgi
W lipcu 1614 w Edynburgu Szkot John Napier (1550-1617) opublikował swe dzieło pt. "Mirifici Logarithmorum Canonis Descriptio". Istnieją dowody, że Napier zajmował się logarytmami już w 1594. Jednak niektórzy historycy twierdzą, że to inny człowiek wynalazł logarytmy przed Napierem, a mianowicie szwajcarski matematyk Joost Bürgi (1552-1632). Bürgi opublikował swe dzieło pt.?Tafeln arithmetischer und mit einer geometrischer Zahlenfolgen gründlichen Erläuterungen, wie sie zu verstehen sind und werden können gebraucht? 6 lat po publikacji Napiera, dopiero w 1620 w Pradze. Sposób przedstawienia logarytmów przez Bürgi?ego różni się w sposób wyraźny od Napiera. Wskazuje to na to, że wynaleźli oni logarytmy zupełnie niezależnie od siebie.

W swojej książce Napier zaproponował ciekawą metodę na mnożenie, dzielenie, potęgowanie i pierwiastkowanie. Wszystkie te działania można było zastąpić o wiele łatwiejszym dodawaniem i odejmowaniem, wykorzystując przy tym właśnie logarytmy.
Dzieło Napiera rozpowszechnił jeden z najsłynniejszych angielskich matematyków - Henry Briggs, profesor geometrii w Gresham College w Londynie. Gdy otrzymał kopię dzieła Napiera w 1614 roku napisał tak: ?Napier skierował moją głowę i ręce do pracy z jego nowymi i niezwykłymi logarytmami. (...) Nigdy wcześniej nie widziałem książki, która tak mnie ucieszyła i wprawiła w podziw?.
Briggs natychmiast zaczął popularyzować ideę logarytmów, a później zaproponował, aby podstawę logarytmów można było zmieniać w celu ułatwienia ich użycia. Do obliczeń logarytmicznych trzeba było używać tabel logarytmicznych, które jednak nie zawierały wszystkich możliwych wyników. Co zatem wtedy robić?
Z pomocą przyszedł tu przyjaciel Briggsa - profesor astronomii w Gresham College - Edmund Gunter. Zaproponował skalę, a w zasadzie linijkę logarytmiczną, którą podzielił na sektory. Zastąpiła ona tabele logarytmiczne.

Edmund Gunter
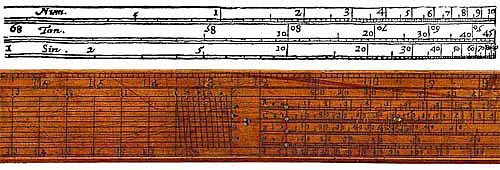
Oryginalny rysunek skali Guntera z 1624r. i drewniana skala Guntera
Niedługo potem William Oughtred (1574-1660) - przyjaciel zarówno Briggsa jak i Napiera ? stworzył ruchomą linijkę logarytmiczną, którą zaczęto nazywać suwakiem logarytmicznym. Oughtred wynalazł również okrągły suwak logarytmiczny, działający tak samo, tylko ruchome skale umieścił na dwóch kołach. Dzieła te stworzył około 1622r., ale do wiadomości publicznej podał swe wynalazki dopiero w 1632r. w książce, pt. ?The Circles of Proportion and the Horizontal instrument?. Zbyt późne opublikowanie pomysłu Oughtreda dało szansę innym, aby go wyprzedzili z pomysłem.

William Oughtred
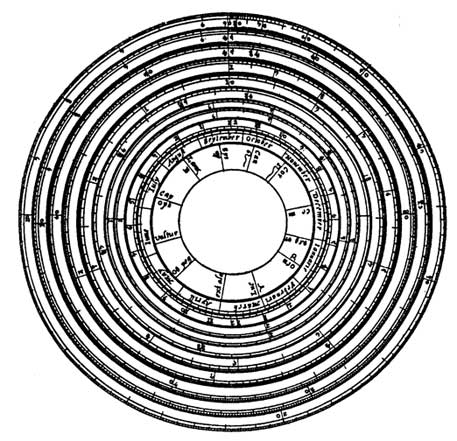
Okrągły suwak Oughtred?a
Oughtred prawdopodobnie opisał swoje urządzenia jednemu ze swych uczniów, co doprowadziło do sytuacji, że Richard Delamain (1600-1644), prywatny nauczyciel matematyki Charles?a I, króla Wielkiej Brytanii i Irlandii, opisał okrągły suwak logarytmiczny w swym dziele "Grammelogia", które zostało wysłane do króla w 1629 roku i opublikowane rok później. Doprowadziło to do werbalnych sporów między Oughtred'em i Delamain'em. Oskarżali się wzajemnie o kradzież wynalazku.
Pierwszy opis logarytmicznej skali Guntera został opublikowany w 1624 roku w Paryżu przez matematyka Edmunda Wingate?a (1596-1656). W 1654 roku Robert Bissaker stworzył ruchomą linijkę mającą 60 cm długości, o przekroju około 6 cm2 i składającą się z 3 skalowanych drewnianych płytek, dwóch nieruchomych i jedną przesuwaną. To już trochę przypominało współczesny suwak logarytmiczny.

Suwak Bissaker'a
Ważnym elementem współczesnego suwaka logarytmicznego jest ruchome okienko, które wprowadził w 1775 roku matematyk John Robertson (1707-1776). A pod koniec XVIII wieku angielski wynalazca James Watt, znany z prac nad silnikiem parowym, skonstruował bardzo dokładny suwak tzw. Soho
![]()
Suwak logarytmiczny Jamesa Watta Soho
Pierwszy nowoczesny suwak stworzył w 1850 roku Victor Mayer Amédée Mannheim (1831-1906), oficer francuskiej artylerii, dodając do suwaka Watt?a dwustronną ruchomą skalę.
Postęp w rozwoju suwaków był coraz większy. Dorzucano coraz więcej skal (nawet do dwudziestu), polepszano jakość materiału, z którego wykonywano suwaki, urozmaicano skale, przez co suwaki zaczęto stosować w wielu dziedzinach życia, m.in.: chemii, inżynierii, biologii, fizyce. Również kształty i rozmiary suwaków zaczęły być bardzo różne, co potem w tym artykule przedstawię.
Na szczególną uwagę zasługują dwa cylindryczne suwaki:
1. Suwak logarytmiczny Fuller?a z 1860 roku ? był odpowiednikiem standardowego suwaka o długości ponad 84 stóp (25 metrów). Można go było utrzymać w rękach, ponieważ miał budowę cylindryczną. Skala logarytmiczna była owinięta wokół cylindrów lub zwinięta w spiralę. Można było na nim wykonywać bardzo dokładne obliczenia.

Suwak Fullera
2. Suwak logarytmiczny Edwina Thacher'a z 1870 roku. Skala logarytmiczna umieszczona była na bębnie i serii poprzeczek. Był odpowiednikiem standardowego suwaka logarytmicznego o długości 18 metrów. Również był bardzo dokładny w obliczeniach. Thacher opatentował go w 1881 roku, a wyprodukowany został przez firmę Keuffel & Esser w Nowym Jorku około 1887 roku.

Suwak Thacher w (1887)
ZASADA DZIAŁANIA SUWAKA LOGARYTMICZNEGO
Teraz przejdźmy do współczesności, a w zasadzie do wieku XX. Urządzenie w dzisiejszej postaci było wykorzystywane przez prawie 150 lat. W latach 80-tych XX w. suwaki zastąpiono kalkulatorami. Ale niektóre ich odmiany są do dziś stosowane i to w wielu dziedzinach życia. Budowa tego urządzenia jest bardzo prosta, przypomina linijkę, ale z nieco inną skalą, tzw. skalą logarytmiczną.
Poniżej zdjęcie klasycznego suwaka logarytmicznego wraz z opisem jego części.

Suwak logarytmiczny działa na zasadzie dodawania logarytmów poprzez dodawanie różnej długości odcinków zaznaczonych na skali. Jest to praktyczne wykorzystanie znanego wzoru:
log (ab) = log (a) + log (b)
Tym samym mnożenie sprowadza się do dodawania, a na suwaku jest to dodawanie odcinków. Suwak logarytmiczny umożliwia więc elementarne obliczenia zawierające mnożenie, dzielenie, logarytmowanie, potęgowanie, pierwiastkowanie. Można również wykonywać za pomocą niego działania na funkcjach trygonometrycznych. Niekiedy posiada dodatkowe znaczniki lub skale pozwalające szybko obliczać powierzchnię koła, ciężar i wytrzymałość prętów itp.
Dokładność obliczeń jest różna w poszczególnych przypadkach. Przeciętnie wyniki otrzymane za pomocą suwaka logarytmicznego o długości 25cm odpowiadają obliczeniom w trzecim stopniu dokładności, tzn. błąd względny zawiera się między 0,1% a 1%.
W Polsce suwaki produkowane były seryjnie przez przedsiębiorstwo Skala najczęściej ze skalą o długości 25 lub 12,5 cm.

Klasyczny suwak logarytmiczny o długości 25cm. Produkowany w Polsce przez firmę SKALA
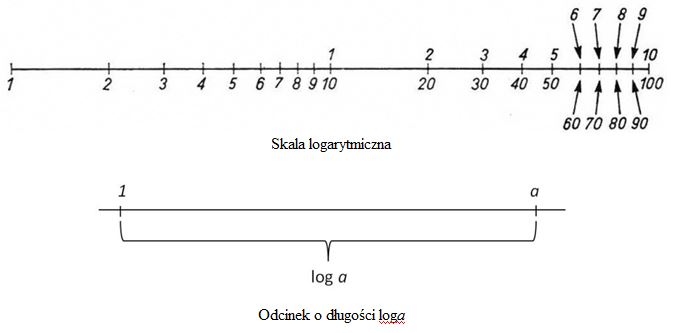
Działanie suwaka opiera się na skali logarytmicznej. Konstrukcja tej skali jest następująca: obieramy pewien odcinek za jednostkę długości, np. 25 cm, odmierzamy od początkowego punktu skali odcinki, których miary przy przyjętej jednostce długości są równe logarytmom dziesiętnym pewnego ciągu liczb, przy czym odmierzając odcinek loga piszemy przy jego końcu liczbę a.
Przy punkcie początkowym należy umieścić liczbę 1, gdyż log1=0. W ten sposób na skali logarytmicznej odległość od punktu 1 do punktu a wynosi w obranej skali loga.
Wiemy, że log10a=1+loga, to każdej liczbie z przedziału od 10 do 100 odpowiada na skali logarytmicznej liczba 10 razy od niej mniejsza. Rozumowanie to może być przeprowadzone także dla każdego przedziału od 10na do 10n+1a. Zatem odcinek równy przyjętej jednostce długości i odpowiadający przedziałowi liczb od 1 do 10 reprezentuje całą nieskończoną skalę logarytmiczną. Liczbom o jednakowym układzie cyfr, lecz różniącym się tylko o czynnik 10n ,np. 6,03; 0,0603; 60300), odpowiada na skali ten sam punkt 6,03.
Skale suwaka
Suwak logarytmiczny składa się z części stałej w postaci linijki, wysuwki poruszającej się w wyżłobieniach linijki oraz okienka ruchomego ze szkiełkiem, na którym zaznaczone są jedna lub trzy rysy. Poniżej standardowe skale.

K ? skala sześcianów liczb, służy jednocześnie do obliczania pierwiastków 3-go stopnia
A ? skala kwadratów liczb, służy jednocześnie dla obliczania pierwiastków kwadratowych
B ? zdublowana skala kwadratów
I ? skala odwrotności (1/x), skierowana w przeciwną stronę (najczęściej oznaczana kolorem czerwonym)
C ? podstawowa skala rachunkowa
D ? podstawowa skala rachunkowa (jak i powyżej), na niej zazwyczaj rozpoczyna się rachunek
L ? skala logarytmów (mantys)
Na odwrotnej stronie wysuwki umieszczona jest skala logarytmiczna dla funkcji trygonometrycznych:
S - sin (sinus)
S&T sin/tg
T ? tg (tangens)
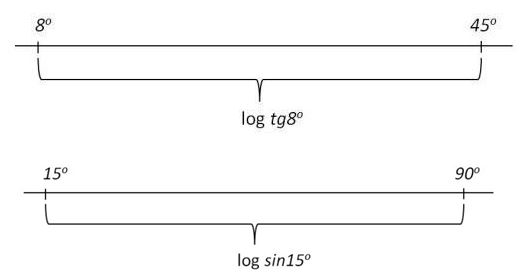
Na skali T punkt początkowy umieszczony jest na prawym końcu; odpowiada mu kąt 45°, gdyż logtg450 = 0. Punktom skali odpowiadają kąty T° mniejsze od 45°, a więc logtgT° <O. Odległość punktu T° od punktu początkowego wynosi |logtg T°| przy obranej jednostce długości. Na lewym końcu skali leży taki punkt To1, dla którego logtg To1=-1.
Na skali S punktowi początkowemu umieszczonemu na końcu skali odpowiada kąt 90°, gdyż
logsin90°=0. Odległość So od punktu początkowego wynosi |logsinSo| przy obranej jednostce długości. Na lewym końcu skali leży punkt So1, dla którego logsinSo1= -1.
Dla kątów mniejszych od 5°44" wartości sinusa i tangensa pokrywają się w granicach dokładności suwaka, dlatego utworzona została wspólna skala S&T.
Aby rozpocząć jakiekolwiek obliczenia na suwaku należy zapoznać się z jego skalami, długością suwaka. Sposób rachowania na suwaku polega na ustawieniu dwóch liczb jednej naprzeciw drugiej na dwóch różnych skalach i odczytaniu wyniku w określonym punkcie jednej skali położonym naprzeciw określonej liczby drugiej skali.
Ważne zasady przy korzystaniu z suwaka
1. Suwak daje tylko układ cyfr wartościowych i za każdym razem trzeba dobrać odpowiedni czynnik 10n (gdzie n jest liczbą całkowitą), czyli ustalić miejsce przecinka dziesiętnego. W tym celu najlepiej jest oszacować w pamięci wynik z grubsza, aby oszacować rząd wielkości wyniku.
2. Przy obliczeniach złożonych nie odczytuje się pośrednich wyników, ale tylko nastawia się na nie każdorazowo środkową rysę ruchomego okienka. Dlatego należy tak dobierać porządek obliczeń, aby wyniki kolejnych działań lub grupy działań były odczytywane na skalach nieruchomych, a nie na wysuwce.
3. W przypadku gdy punkt a wysuwki, naprzeciw którego ma się znaleźć wynik na skali nieruchomej, wychodzi poza granicę tej skali, należy nastawić rysę okienka na jeden z końców skali, wysuwki, a następnie przerzucić wysuwkę w taki sposób, aby pod rysą okienka znalazł się drugi koniec skali wysuwki. Wówczas szukany wynik, który ma być na wprost punktu a podziałki, okaże się w granicach skali nieruchomej i będzie mógł być odczytany.
Poniżej ważniejsze schematy na zastosowanie suwaka logarytmicznego:
Mnożenie, dzielenie, proporcje
Schemat 1
Schemat 2
Schemat 3
Schemat 4
Schemat 5
Schemat 6
Schemat 7
Schemat 8
Potęgowanie, pierwiastkowanie
Schemat 9
Schemat 10
Logarytmowanie
Schemat 11
Obliczenia trygonometryczne
Schemat 12
Schemat 13
To podstawowe zastosowanie suwaka. Oprócz tego możemy zamieniać stopnie na radiany i odwrotnie, obliczać pole koła i wiele innych działań.
Suwaki logarytmiczne stosowane były w różnych dziedzinach życia i przyjmowały różne kształty jak i różne skale, co można zobaczyć poniżej.
KLASYCZNE LINIOWE SUWAKI LOGARYTMICZNE

Ja z dydaktycznym ściennym suwakiem logarytmicznym.
Takie suwaki wisiały w szkolnych klasach i były używane do lat 80-tych ubiegłego wieku.
Produkowała je Polska Fabryka Pomocy Naukowych BIOFIZ w Kętach. Suwak pochodzi z 1960r.

Polski suwak firmy SKALA 1973r.

Angielski suwak Wollaston do obliczeń chemicznych

Amerykański suwak firmy Acumath 1959r.

Niemiecki suwak firmy De Muiderkring 1963r.

Amerykański suwak firmy Howitzer 1972r. - używany przez amerykańską armię podczas wojny w Wietnamie

Angielski suwak firmy W&S Jones - 1792r.

Angielski suwak Dring&Fage - 1868r.
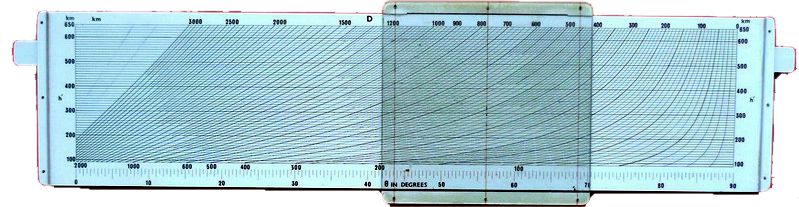
Australijski suwak firmy White&Gillespie - 1792r.

Angielski suwak Thornton F5100

Suwak w ołówku
CYLINDRYCZNE SUWAKI LOGARYTMICZNE

Angielskie suwaki Otis King 1921r.

Szwajcarski suwak firmy Daemon-Schmid 1930r.

Szwajcarski suwak firmy Daemon-Schmid 1915r.

Australijski suwak firmy C.O. Browne
KOŁOWE SUWAKI LOGARYTMICZNE

Polski suwak stosowany w wojskach artyleryjskich

Niemiecki suwak firmy Controller Calculator KG 1961r.

Rosyjski suwak używany w wojskach artyleryjskich

Francuski suwak Charpentier Calculimetre

Angielskie suwaki firmy William H. Fowler 1900r.

Amerykański suwak firmy G.Small 1918r.

Amerykański suwak stworzony przez Johna Browna

Australijski suwak stosowany w lotnictwie

Suwak logarytmiczny dla obliczania wskaźnika BMI (ang. Body Mass Index), czyli współczynnika masy ciała
SUWAKI LOGARYTMICZNE W ZEGARKACH
SUWAKI LOGARYTMICZNE W ŻYCIU

Budynek Wydziału Fizyki i Matematyki Bashkir State University w kształcie suwaka logarytmicznego

Po tym jak kalkulatory wyparły suwaki Werner Rudowski stworzył w 1989 roku pomnik
"Śmierć suwaka logarytmicznego"

Studenckie centrum nauki

Pilot podczas nawigacji używał specjalnej wersji suwaka dla lotnictwa

Mikhail Kalashnikov - wynalazca słynnego karabinu maszynowego AK

Spinka do krawatu w kształcie suwaka logarytmicznego

Bransoleta na rękę (obecnie produkowana)

Pojemnik na ołówki
Kubki i kufle

Suwaki na znaczkach pocztowych
SUWAK LOGARYTMICZNY DO WŁASNEGO WYKONANIA
Zachęcam do zrobienia własnego suwaka z papieru
wg schematu z czasopisma Świat Nauki z 2006
kliknij na obrazek w celu pobrania
Zachęcam do zabawy z wirtualnym suwakiem
kliknij na obrazek
Popularność suwaka ciągle trwa, co potwierdzają aplikacje do telefonów komórkowych:

LINKI/BIBLIOGRAFIA
Światowe muzeum suwaków logarytmicznych
Muzeum suwaków Politechniki Warszawskiej
Poradnik Encyklopedyczny MATEMATYKA - PWN 1986r.
2014 by Tomasz Grębski