Słynne konstrukcje niewykonalne za pomocą cyrkla i liniału
Konstrukcje klasyczne wykonujemy, używając jako przyrządów wyłącznie cyrkla i liniału (czyli linijki bez podziałki).
Jedną z takich konstrukcji jest kwadratura koła.
KWADRATURA KOŁA - problem polegający na skonstruowaniu kwadratu, którego pole równe jest polu danego koła przy użyciu wyłącznie cyrkla i linijki bez podziałki. Jest to jeden z trzech wielkich problemów starożytnej matematyki greckiej (obok trysekcji kąta i podwojenia sześcianu), sformułowany przez szkołę pitagorejską.
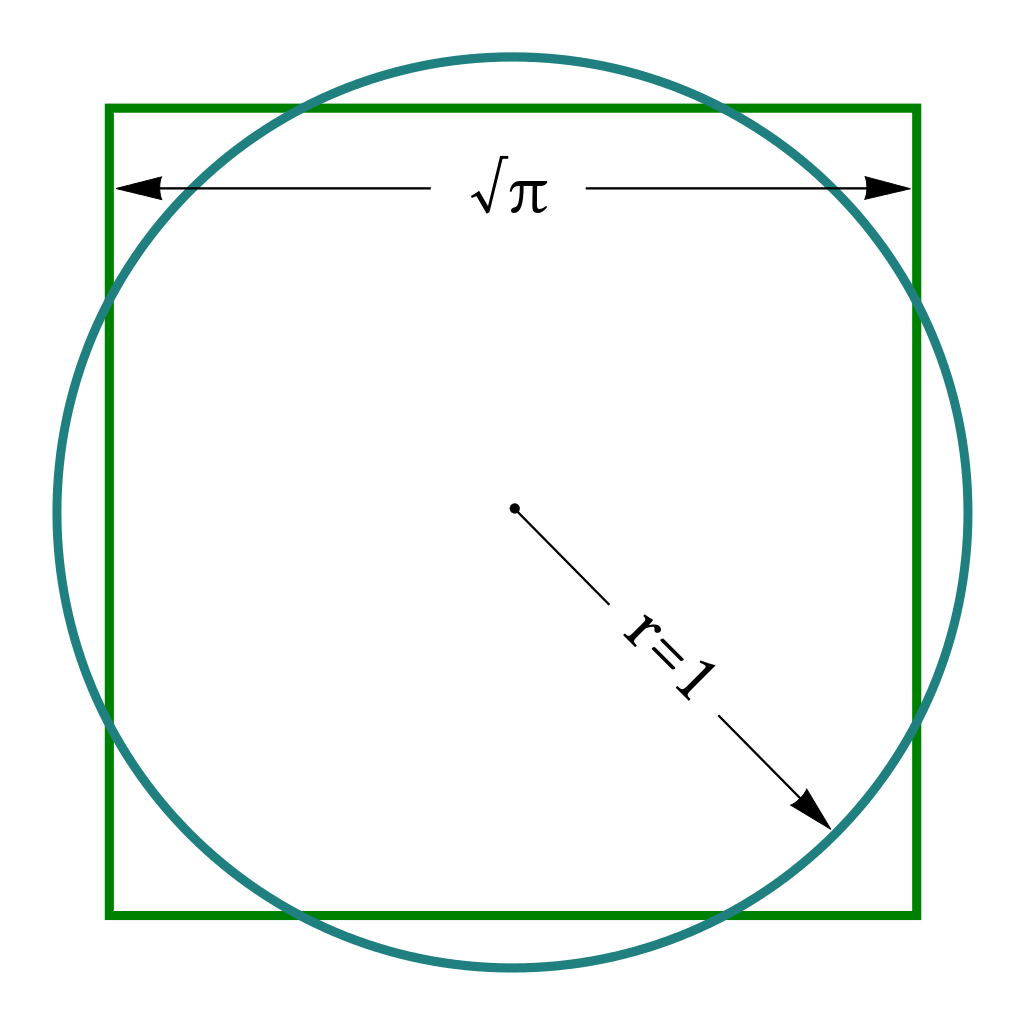
Konstrukcja taka jest niewykonalna – wynika to z twierdzenia udowodnionego w roku 1837 przez Pierre'a Wantzela oraz faktu wykazanego w 1882 roku przez Ferdinanda Lindemanna, iż π jest liczbą przestępną.

Pierre Laurent Wantzel
(ur. 5 czerwca 1814 w Paryżu, zm. 21 maja 1848 w Paryżu)

Carl Louis Ferdinand von Lindemann
(ur. 12 kwietnia 1852 w Hanowerze, zm. 6 marca 1939 w Monachium)
Pierwsze próby kwadratury koła sięgają Starożytnego Egiptu, opisane zostały jako problem 48 w Papirusie Rhinda, gdzie opisana została aproksymacja kwadratury koła.

Papirus Rhinda (ang. Rhind papyrus, rzadziej Ahmes papyrus (pol. „papirus Ahmesa”), także Rhind Mathematical Papyrus, RMP) – jeden z najstarszych znanych dokumentów matematycznych, sporządzony w XVII w. p.n.e. przez królewskiego skrybę Ahmesa, zawierający przykłady rozwiązań dla problemów matematycznych z zakresu algebry i geometrii. Jego nazwa pochodzi od nazwiska jego odkrywcy – brytyjskiego egiptologa Alexandra Henry'ego Rhinda (1833–1863), który zakupił go w 1858 roku. Dwie części papirusu przechowywane są w Muzeum Brytyjskim w Londynie, a niewielkie jego fragmenty znajdują się w Brooklyn Museum w Nowym Jorku.
Kwadratura koła jest bezpośrednio związana z rektyfikacją okręgu: gdyby jedna z tych konstrukcji była wykonalna, oznaczałoby to, że wykonalna jest także druga.
Określenie kwadratura koła funkcjonuje również w języku potocznym i oznacza coś niewykonalnego, z góry skazanego na niepowodzenie.
Mimo niewykonalności konstrukcji, niektórzy wciąż próbują...

Bibliografia:
Hans Niels Jahnke: A history of analysis. Providence, RI: American Mathematical Society, 2003, s. 15.
Matematyka, Warszawa: Wydawnictwa Szkolne i Pedagogiczne, 1990 (Encyklopedia szkolna), s. 116
http://www.archaeowiki.org/Image:Rhind_Mathematical_Papyrus.jpg (https://www.britishmuseum.org/, British Museum)
O'Connor J.J., Robertson E.F., Squaring the circle, MacTutor History of Mathematics archive

