TWIERDZENIE
Przypuśćmy, że w pewnej grupie ludzi każda para przyjaciół ma dokładnie jednego wspólnego przyjaciela. Wtedy z pewnością istnieje osoba, która jest przyjacielem wszystkich.
W matematycznym żargonie twierdzenie to nazywa się twierdzeniem o przyjaźni.
Zanim zmierzymy się z dowodem, przełóżmy wszystko na język teorii grafów. Osoby z rozważanej grupy utożsamiamy z wierzchołkami pewnego grafu. Dwa wierzchołki łączymy krawędzią wtedy i tylko wtedy, kiedy odpowiednie osoby się przyjaźnią. Zakładamy po cichu, że przyjaźń jest zawsze obustronna, tzn. jeśli \(u\) jest przyjacielem \(v\), to i \(v\) jest przyjacielem \(u\). Twierdzenie przybiera więc następującą postać.
Twierdzenie.
Przypuścmy, ze\(G\) jest grafem, w którym dowolna para wierzchołków ma dokładnie jednego wspólnego sąsiada. Istnieje wówczas wierzchołek, który sąsiaduje ze wszystkimi innymi wierzchołkami.
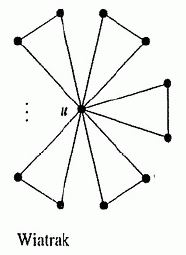
Zauważmy, że wspomnianą własność mają np. grafy przedstawione na rysunku poniżej (przyjacielem jest \(u\) ); pokażemy, że takie „wiatraki” są w istocie jedynymi grafami, których dotyczy twierdzenie.
Znanych jest kilka dowodów twierdzenia o przyjaźni, jednak pierwszy, autorstwa Paula Erdósa, Alfreda Rényiego i Very Sós, wciąż wydaje się najbliższy ideału.
Dowód.
Przypuśćmy, że teza jest fałszywa; niech \( G\) stanowi kontrprzykład (tzn. żaden z wierzchołków \(G\) nie sąsiaduje ze wszystkimi pozostalymi). Rozumowanię wiodące do sprzeczności składa się z dwóch kroków. Pierwsza część dowodu to kombinatoryka, druga zaś - algebra liniowa.
(1) Twierdzimy, że \(G\) jest grafem regularnym, tj. \(d(u)=d(v)\) dla dowolnej pary wierzchołków \(u, v \in V\). Zauważmy, że z założenia wynika tak zwany warunek \(C_4\) : w \(G\) nie ma cykli długości 4 .
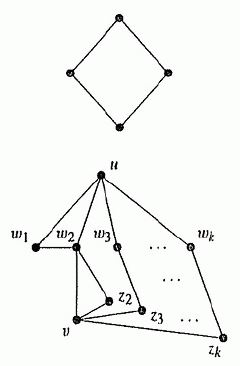
Wykażemy najpierw, że jeśli \(u\) i \(v\) nie są sąsiednimi wierzchołkami, to mają równe stopnie, \(d(u)=d(v)\). Przypuśćmy, że \(d(u)=k\) i niech \(w_1, \ldots, w_k\) będą sąsiadami \(u\). Dokładnie jeden z nich, powiedzmy \(w_2\), jest sąsiadem \(v\); co więcej, \(w_2\) sqasiaduje z dokładnie jednym spośród pozostalych \(w_i\), powiedzmy z \(w_1\) - mamy więc do czynienia z sytuacją przedstawioną na rysunku:
Wierzchołek \(v\) ma z \( w_1\) wspólnego sąsiada \(w_2\), a \(\mathrm{z}\) każdym spośród \(w_i(i \geq 2)\) wspólnego sq̨siada \(z_i(i \geq 2)\). Na mocy warunku \(C_4\), wszystkie \(z_i\) sq̨ różne. Wynika stąd, że \(d(v) \geq k=d(u)\), a więc \(d(u)=d(v)=k\) dzięki symetrii rozważań.
Aby ukończyć dowód (1), zauważmy, że dowolny wierzchołck różny od \(w_2\) nie sąsiaduje z \(u\) lub nie sąsiaduje z \(v\), więc zgodnie z tym, co przed chwilą udowodnilísmy, jego stopień jest równy \(k\). Jednak również \(w_2\) nie sasiaduje z pewnym wierzchołkiem \({ }^1\), zatem stopień \(w_2\) też jest równy \(k\), a to oznacza, że \(G\) jest grafem \(k\)-regularnym.
Sumując stopnie wszystkich \(k\) sąsiadów \(u\), otrzymujemy wynik \( k^2\). Ponieważ każdy wierzchołek (różny od \(u\) ) ma z \(u\) dokładnie jednego wspólnego sąsiada, więc policzylísmy każdy wierzchołek jeden raz, wyjąwșzy \(u\), który został policzony \(k\)-krotnie. Zatem liczba wszystkich wierzchołków grafu \(G\) wynosi
\[
n=k^2-k+1 .
\]
(2) Reszta dowodu to piękne zastosowanie standardowych twierdzeń algebry liniowej. Zauważmy po pierwsze, że \(k\) musi być większe od 2, gdyż dla \(k \leq 2\) na mocy (1) dopuszczone są tylko \(G=K_1\) i \(G=K_3\), czyli dwa trywialne wiatraki. Rozważmy macierz sąsiedztwa \(\mathbf{A}=\left(a_{i j}\right)\), zdefiniowaną na stronie 243 . Z pierwszej części dowodu wynika, że w każdym jej wierszu jest dokładnie \(k\) jedynek, natomiast z założeń twierdzenia wnosimy, że dla każdych dwóch wierszy istnieje dokładnie jedna kolumna, w której w obu wierszach figuruje jedynka. Ponadto na głównej przekątnej są same zera. Mamy zatem
\[
\mathbf{A}^2=\left(\begin{array}{cccc}
k & 1 & \ldots & 1 \\
1 & k & & 1 \\
\vdots & & \ddots & \vdots \\
1 & \ldots & 1 & k
\end{array}\right)=(k-1) \mathbf{I}+\mathbf{J}
\]
gdzie \(I\) jest macierzą identycznościową, \(J\) zaś - mácierzą z samych jedynek. Sprawdzamy natychmiast, że \(J\) ma wartości własne \(n\) (krotności 1) i 0 (krotnosci \(n-1)\). Wartościami własnymi macierzy \(\mathbf{A}^2\) są więc \(k-1+n=k^2\) oraz \(k-1\); ich krotnościami są odpowiednio 1 i \(n-1\).
\(A\) jest symetryczna, a zatem diagonalizowalna. Wnosimy stąd, że \(A\) ma wartości własne \(k\) (krotności 1) oraz \(\pm \sqrt{k-1}\). Przypuśćmy, że jest \(r\) wartości własnych równych \(\sqrt{k-1}\) i \(s\) równych \(-\sqrt{k-1}\), gdzie \(r+s=n-1\). Jesteśmy już bardzo blisko celu. Ponieważ suma wartosci własnych macierzy \(A\) jest równa jej śladowi (czyli 0), więc mamy
\[
k+r \sqrt{k-1}-s \sqrt{k-1}=0 .
\]
W szczególności, \(r \neq s \mathrm{}\) i
\[
\sqrt{k-1}=\frac{k}{s-r} .
\]
Wynika stąd, że \(\sqrt{k-1}\) jest liczbą całkowitą \(h\) (jeśli liczba \(\sqrt{m}\) jest wymierna, to jest całkowita). Otrzymujemy
\[
h(s-r)=k=h^2+1 .
\]
Skoro \(h\) dzieli jednocześnie \( h^2+1 \) i \( h^2\), musi być jedynką, a zatem \(k=h^2+1=2\), choć tę ewentualność wykluczyliśmy wcześniej. Otrzymaliśmy więc sprzeczność, która kończy cały dowód.
Na tym jednak nie koniec historii. Przeformułujmy twierdzenie w następujący sposób:
Niech \(G\) będzie grafem, w którym dowolne dwa wierzchołki łączy dokładnie jedna droga długości 2 (to oczywiście równoważna wersja warunku przyjaźni); wtedy \(G\) musi być wiatrakiem. A co się stanie, gdy zaczniemy rozważać drogi o długości większej od 2? Wedle hipotezy, którą sformułował Anton Kotzig, nie ma tu nic do rozważania, gdyż odpowiednie grafy po prostu nie istnieją.
Hipoteza Kotziga.
Niech \(\ell>2\). Wtedy nie istnieje żaden graf, w którym każde dwa wierzcholki bylyby połączone dokładnie jedną drogą długości \(l\).
Sam Kotzig sprawdził, że hipoteza jest prawdziwa dla \(\ell \leq 8\). Za pomocą niezwykle sprytnego zliczania Xing i Hu wykazali jej prawdziwość dla wszystkich \(\ell \geq 12\), a dowód pozostałych przypadków podali Yang, Lin, Wang i Li. Hipoteza Kotziga jest więc dziś twierdzeniem.
Bibliografia
[1] P. Erdós, A. Rényi, V. Sós: On a problem of graph theory, Studia Sci. Math. Hungar: 1 (1966), 215-235.
[2] A. Korzig: Regularly k-path connected graphs, Congressus Numerantium 40 (1983), 137-141.
[3] K. XING, B. HU: On Kotzig's conjecture for graphs with a regular pathconnectedness, Discrete Math. 135 (1994), 387-393.
[4] Y. YANG, J. LIN, C. WANG, V. LI: On Kotzig's conjecture concerning graphs with a unique regular path-connectivity, Discrete Math. 211 (2000), 287-298.
[5] M. AIGNER, G.M.ZIEGER: Dowody z księgi, PWN, Warszawa 2002