Zadanie 1. [2021 Informator CKE, zad.2, 3 pkt]
Dane są liczby $$a=\left(\log _{\sqrt{5}} 2\right) \cdot \log _2 25$$ i $$b=\frac{\log _5 6}{\log _5 8}$$. Oblicz $$a^{b+1}$$
Obliczamy $$a$$ oraz $$b$$ z wykorzystaniem wzoru na zamianę podstawy logarytmu:
$$\begin{aligned}&a=\log _{\sqrt{5}} 2 \cdot \log _2 25=\frac{\log _2 2}{\log _2 \sqrt{5}} \cdot 2 \log _2 5=\frac{\log _2 2}{\frac{1}{2} \log _2 5} \cdot 2 \log _2 5=4 \\&b=\frac{\log _5 6}{\log _5 8}=\log _8 6=\frac{\log _2 6}{\log _2 8}=\frac{1}{3} \log _2 6=\log _2 \sqrt[3]{6}\end{aligned}$$
Obliczamy $$a^{b+1}$$ :
$$a^{b+1}=4^{\log _2 \sqrt[3]{6}+1}=4^{\log _2 \sqrt[3]{6}} \cdot 4^1=2^{2 \log _2 \sqrt[3]{6}} \cdot 4=2^{\log _2 \sqrt[3]{36}} \cdot 4=4 \sqrt[3]{36}$$
Zadanie 2. [2022 marzec, zad.1, 3 pkt]
Dane są liczby $$a=\log _2 3$$ oraz $$b=\log _3 7$$.
Wyraź $$\log _4 49$$ za pomocą liczb $$a$$ oraz $$b$$.
Zapisz obliczenia.
$$\log _4 49=2 \cdot \log _4 7=2 \cdot \frac{\log _3 7}{\log _3 4}=2 \cdot \frac{\log _3 7}{\frac{\log _2 4}{\log _2 3}}=2 \cdot \log _3 7 \cdot \frac{\log _2 3}{\log _2 4}=2 \cdot \log _3 7 \cdot \frac{\log _2 3}{2}$$
Zatem
$$\log _4 49=2 \cdot b \cdot \frac{a}{2}=a \cdot b$$
Odp. $$\log _4 49=a \cdot b$$.
Zadanie 3. [2022 Zbiór zadań CKE, zad.1, 3 pkt]
Oblicz wartość wyrażenia
$$
\log _8 3^{3 \log _3 2-\log _{27} 8-\log _9 4}
$$
Zapisz obliczenia.
Stosujemy wzór na zamianę podstaw logarytmu i przekształcamy wykładnik potęgi
$$
3 \log _3 2-\log _{27} 8-\log _9 4=3 \log _3 2-\log _{3^3} 8-\log _{3^2} 4=3 \log _3 2-\frac{1}{3} \log _3 8-\frac{1}{2} \log _3 4
$$
Stosujemy wzór na logarytm potęgi
$$
\begin{gathered}
3 \log _3 2-\frac{1}{3} \log _3 8-\frac{1}{2} \log _3 4=3 \log _3 2-\frac{1}{3} \log _3 2^3-\frac{1}{2} \log _3 2^2= \\
=3 \log _3 2-\frac{1}{3} \cdot 3 \log _3 2-\frac{1}{2} \cdot 2 \log _3 2=\log _3 2
\end{gathered}
$$
Stosując wzór $$a^{\log _a b}=b$$, obliczamy wartość potęgi
$$
\log _8 3^{3 \log _3 2-\frac{1}{3} \log _3 8-\frac{1}{2} \log _3 4}=\log _8 3^{\log _3 2}=\log _8 2=\frac{1}{3}
$$
Zadanie 4. [2022 Zbiór zadań CKE, zad.6, 3 pkt]
W rozwinięciu wyrażenia $$(a+b)^n$$ dla pewnego $$n \in N$$ suma współczynników przy wyrazach $$a^{n-2} b^2$$ oraz $$a^{n-1} b$$ jest równa 66.
Oblicz n. Zapisz obliczenia.
Stosujemy wzór na rozwinięcie dwumianu Newtona:
$$
(a+b)^n=\left(\begin{array}{l}
n \\
0
\end{array}\right) a^n b^0+\left(\begin{array}{l}
\boldsymbol{n} \\
1
\end{array}\right) \boldsymbol{a}^{n-1} \boldsymbol{b}^1+\left(\begin{array}{l}
\boldsymbol{n} \\
2
\end{array}\right) \boldsymbol{a}^{n-2} \boldsymbol{b}^2+\cdots+\left(\begin{array}{c}
n \\
n-1
\end{array}\right) a^1 b^{n-1}+\left(\begin{array}{l}
n \\
n
\end{array}\right) a^0 b^n
$$
Zapisując sumę współczynników przy odpowiednich potęgach, otrzymujemy równanie:
$$
\left(\begin{array}{l}
n \\
2
\end{array}\right)+\left(\begin{array}{l}
n \\
1
\end{array}\right)=66
$$
Stosujemy wzór na symbol Newtona $$\left(\begin{array}{l}n \\ k\end{array}\right)$$, skąd po przekształceniach otrzymujemy kolejno:
$$
\begin{aligned}
&\frac{(n-1) n}{2}+n=66 \\
&n^2+n-132=0
\end{aligned}
$$
Rozwiązujemy równanie kwadratowe i sprawdzamy, które z rozwiązań jest liczbą naturalną:
$$
n=-12 \notin N \text { oraz } n=11 \in N
$$
Szukanym wykładnikiem jest $$n=11$$.
Zadanie 5. [2022 grudzień, zad.1, 2 pkt]
Oblicz
$$
\frac{\log _3 5 \cdot \log _{25} 27}{\log _7 \sqrt[6]{49}}
$$
Zapisz obliczenia.
Stosujemy wzór na zamianę podstawy logarytmu i otrzymujemy
$$
\frac{\log _3 5 \cdot \log _{25} 27}{\log _7 \sqrt[6]{49}}=\frac{\log _3 5 \cdot \frac{\log _3 27}{\log _3 25}}{\log _7 \sqrt[6]{49}}=\frac{\log _3 5 \cdot \frac{\log _3 27}{\log _3 5^2}}{\log _7\left(7^2\right)^{\frac{1}{6}}}
$$
Stosujemy wzór na logarytm potęgi i korzystamy z definicji logarytmu, otrzymując
$$
\frac{\log _3 5 \cdot \frac{\log _3 27}{\log _3 5^2}}{\log _7\left(7^2\right)^{\frac{1}{6}}}=\frac{\log _3 5 \cdot \frac{3}{2 \log _3 5}}{\frac{1}{3} \log _7 7}=\frac{\frac{3}{2}}{\frac{1}{3}}=\frac{9}{2}
$$
Zadanie 6. [2023 maj, zad.1, 2 pkt]
W chwili początkowej $$(t=0)$$ masa substancji jest równa 4 gramom. Wskutek rozpadu cząsteczek tej substancji jej masa się zmniejsza. Po każdej kolejnej dobie ubywa $$19 \%$$ masy, jaka była na koniec doby poprzedniej. Dla każdej liczby całkowitej $$t \geq 0$$ funkcja $$m(t)$$ określa masę substancji w gramach po $$t$$ pełnych dobach (czas liczymy od chwili początkowej).
Wyznacz wzór funkcji $$m(t)$$. Oblicz, po ilu pełnych dobach masa tej substancji będzie po raz pierwszy mniejsza od 1,5 grama. Zapisz obliczenia.
Oznaczmy:
$$t$$ - czas (w dobach), licząc od chwili początkowej,
$$m(t)$$ - masa substancji po $$t$$ dobach, licząc od chwili początkowej.
Liczby $$m(0), m(1), m(2)$$ itd. są kolejnymi wyrazami ciągu geometrycznego o ilorazie 0,81 . Zatem
$$
m(t)=4 \cdot 0,81^t
$$
gdzie $$t$$ jest liczbą całkowitą nieujemną. Ten ciąg geometryczny jest malejący. Ponadto
$$
\begin{aligned}
& m(4)=4 \cdot 0,81^4 \approx 1,72>1,5 \\
& m(5)=4 \cdot 0,81^5 \approx 1,39<1,5
\end{aligned}
$$
więc masa substancji będzie mniejsza od $$1,5 \mathrm{~g}$$ po pięciu dobach.
Zadanie 7. [2023 czerwiec, zad.1, 2 pkt]
Dane są liczby
$$
a=4^{\log _2 45} \quad \text { oraz } \quad b=\frac{\log _3 2023}{\log _9 2023}
$$
Oblicz $$a-b$$.
Obliczamy $$a$$ :
$$
a=4^{\log _2 45}=\left(2^2\right)^{\log _2 45}=2^{\log _2 45^2}=45^2=2025
$$
Stosujemy wzór na zamianę postawy logarytmu i obliczamy $$b$$ :
$$
b=\frac{\log _3 2023}{\log _9 2023}=\frac{\log _3 2023}{\frac{\log _3 2023}{\log _3 9}}=\log _3 9=2
$$
Zatem $$a-b=2023$$.
Zadanie 8. [2024 maj, zad.1, 2 pkt]
W chwili początkowej \((t=0)\) filiżanka z gorącą kawą znajduje się w pokoju, a temperatura tej kawy jest równa \(80^{\circ} \mathrm{C}\). Temperatura w pokoju (temperatura otoczenia) jest stała i równa \(20^{\circ} \mathrm{C}\). Temperatura \(T\) tej kawy zmienia się w czasie zgodnie z zależnością
\[T(t)=\left(T_{p}-T_{z}\right) \cdot k^{-t}+T_{z} \quad \text { dla } \quad t \geq 0\]
gdzie:
\(T\) - temperatura kawy wyrażona w stopniach Celsjusza,
\(t\) - czas wyrażony w minutach, liczony od chwili początkowej,
\(T_{p}\) - temperatura początkowa kawy wyrażona w stopniach Celsjusza,
\(T_{z}\) - temperatura otoczenia wyrażona w stopniach Celsjusza,
\(k\) - stała charakterystyczna dla danej cieczy.
Po 10 minutach, licząc od chwili początkowej, kawa ostygła do temperatury \(65^{\circ} \mathrm{C}\).
Oblicz temperaturę tej kawy po następnych pięciu minutach. Wynik podaj w stopniach Celsjusza, w zaokrągleniu do jedności. Zapisz obliczenia.
Z warunków zadania \(T(10)=65\), więc \(65=(80-20) \cdot k^{-10}+20\) i stąd \(k^{-10}=\frac{45}{60}=\frac{3}{4}\). Zatem
\[\begin{aligned}
T(15) & =(80-20) \cdot k^{-15}+20=60 \cdot\left(k^{-10}\right)^{1,5}+20= \\
& =60 \cdot\left(\frac{3}{4}\right)^{1,5}+20=60 \cdot \frac{3}{4} \cdot \frac{\sqrt{3}}{2}+20=\frac{45 \sqrt{3}}{2}+20 \approx 59
\end{aligned}\]
Temperatura kawy po następnych pięciu minutach była równa \(59^{\circ} \mathrm{C}\).
Zadanie 9. [2024 maj, zad.5, 3 pkt]
Wykaż, że jeżeli \(\log _{5} 4=a\) oraz \(\log _{4} 3=b\), to \(\log _{12} 80=\frac{2 a+1}{a \cdot(1+b)}\).
Przekształcamy wyrażenie \(\log _{12} 80\), stosując wzór na zamianę podstawy logarytmu, a następnie wzór na logarytm iloczynu:
\[\log _{12} 80=\frac{\log _{4}(16 \cdot 5)}{\log _{4}(4 \cdot 3)}=\frac{\log _{4} 16+\log _{4} 5}{\log _{4} 4+\log _{4} 3}=\frac{2+\log _{4} 5}{1+\log _{4} 3}\]
Korzystamy ze wzoru na zamianę podstawy logarytmu oraz z założenia i otrzymujemy
\[\log _{4} 5=\frac{\log _{5} 5}{\log _{5} 4}=\frac{1}{\log _{5} 4}=\frac{1}{a}\]
Zatem
\[\log _{12} 80=\frac{2+\log _{4} 5}{1+\log _{4} 3}=\frac{2+\frac{1}{a}}{1+b}=\frac{2 a+1}{a \cdot(1+b)}\]
To należało wykazać.
Zadanie 10. [2024 czerwiec, zad.1, 2 pkt]
W chwili początkowej \((t=0)\) zainicjowano pewną reakcję chemiczną, w której brał udział związek A.
W wyniku tej reakcji masa \(m\) związku A zmieniała się w czasie zgodnie z zależnością
\[m(t)=a \cdot 2^{-0,05 \cdot t}+b \quad \text { dla } \quad t \geq 0\]
gdzie:
\(m\) - masa związku A wyrażona w gramach,
\(t\) - czas wyrażony w sekundach (liczony od chwili \(t=0\) ),
\(a, b\) - współczynniki liczbowe.
Masa początkowa związku A (tj. masa w chwili \(t=0\) ) była równa \(m_{0}\) gramów.
Po osiągnięciu stanu równowagi (tj. gdy \(t \rightarrow \infty\) ) masa tego związku była równa \(\frac{1}{9}\) jego masy początkowej (zobacz rysunek).
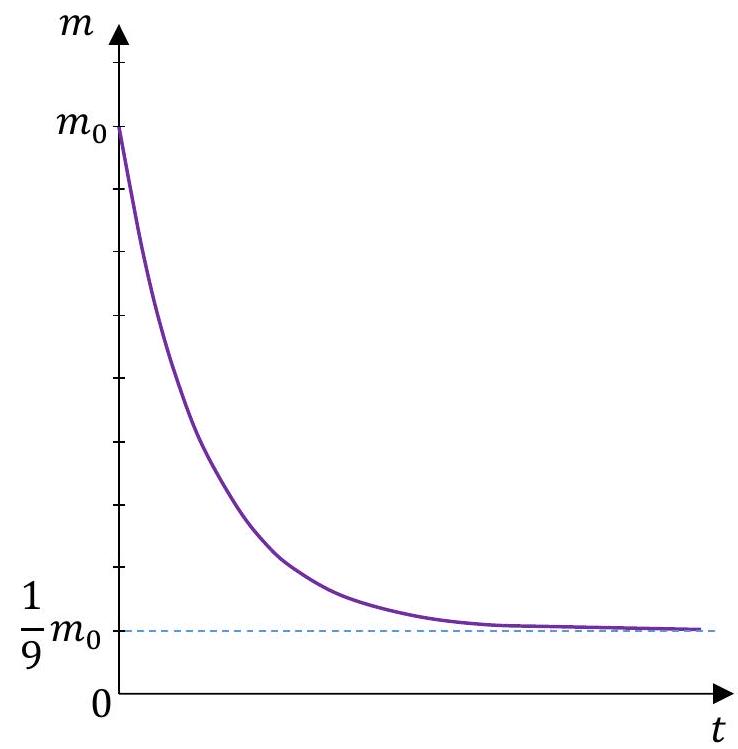
Oblicz, po ilu sekundach (licząc od chwili zainicjowania tej reakcji) przereagowało \(87,5 \%\) masy początkowej tego związku. Zapisz obliczenia.
Ponieważ po osiągnięciu stanu równowagi masa związku A była równa \(\frac{1}{9} m_{0}\), więc
\[\frac{1}{9} m_{0}=\lim _{t \rightarrow+\infty} m(t)=\lim _{t \rightarrow+\infty} a \cdot 2^{-0,05 \cdot t}+b=0+b=b\]
Stąd i \(z\) warunku \(m(0)=m_{0}\) otrzymujemy
\[m_{0}=a \cdot 2^{-0,05 \cdot 0}+\frac{1}{9} m_{0}\]
czyli \(a=\frac{8}{9} m_{0}\).
Obliczamy czas, po którym pozostało \(12,5 \%\) początkowej masy związku A:
\[\begin{gathered}
\frac{1}{8} m_{0}=\frac{8}{9} m_{0} \cdot 2^{-0,05 \cdot t}+\frac{1}{9} m_{0} \quad /: m_{0} \\
\frac{1}{72}=\frac{8}{9} \cdot 2^{-0,05 \cdot t} \\
2^{-6}=2^{-0,05 \cdot t} \\
6=0,05 t \\
t=120
\end{gathered}\]
Zatem po 120 sekundach przereaguje \(87,5 \%\) masy początkowej związku A.
Zadanie 11. [2024 grudzień, zad.1, 2 pkt]
Ładunek elektryczny zgromadzony w kondensatorze można opisać zależnością
\[
Q(t)=Q_{0} \cdot \beta^{-t} \quad \text { dla } \quad t \geq 0
\]
gdzie:
\(Q_{0}\) - ładunek elektryczny zgromadzony w kondensatorze w chwili początkowej \((t=0)\) wyrażony w milikulombach
\(Q\) - ładunek elektryczny zgromadzony w kondensatorze w chwili \(t\) (licząc od chwili początkowej) wyrażony w milikulombach
\(\beta\) - stała dodatnia
\(t\) - czas wyrażony w sekundach.
Wiadomo, że w chwili \(t=4 \mathrm{~s} \mathrm{}\) wkondensatorze był zgromadzony ładunek 2 milikulombów, a w chwili \(t=6 \mathrm{~s}\)-ładunek 18 milikulombów.
1. Oblicz, ile milikulombów ładunku było zgromadzone w tym kondensatorze w chwili \(t=5 \mathrm{~s}\). Zapisz obliczenia.
Sposób I
Z warunków \(Q(4)=2\) oraz \(Q(6)=18\) otrzymujemy związki \(2=Q_{0} \cdot \beta^{-4}\) oraz \(18=Q_{0} \cdot \beta^{-6}\). Stąd
\[
\begin{gathered}
\frac{2}{18}=\frac{Q_{0} \cdot \beta^{-4}}{Q_{0} \cdot \beta^{-6}} \\
\frac{1}{9}=\beta^{2} \\
\beta=\frac{1}{3}
\end{gathered}
\]
Zatem \(2=Q_{0} \cdot\left(\frac{1}{3}\right)^{-4}\), więc \(Q_{0}=\frac{2}{81}\).
Obliczamy \(Q(5)\) :
\[
Q(5)=\frac{2}{81} \cdot\left(\frac{1}{3}\right)^{-5}=\frac{2}{81} \cdot 3^{5}=6
\]
Sposób II
Zauważamy, że ciąg wartości funkcji \(Q\) dla kolejnych liczb naturalnych, tj. \(Q(1), Q(2)\), \(Q(3), \ldots\), jest geometryczny, ma wszystkie wyrazy dodatnie, pierwszy wyraz równy \(Q_{0}\) oraz iloraz \(\frac{1}{\beta}\).
Z własności ciągu geometrycznego otrzymujemy
\[
\begin{gathered}
{[Q(5)]^{2}=Q(4) \cdot Q(6)} \\
{[Q(5)]^{2}=2 \cdot 18} \\
Q(5)=6
\end{gathered}
\]
W chwili \(t=5 \mathrm{~s}\) w kondensatorze był zgromadzony ładunek 6 milikulombów.
Zadanie 12. [2025 maj, zad.1, 2 pkt]



