Zadanie 1. [2021 Informator CKE, zad.1, 1 pkt]
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Wartość wyrażenia $$2021$$: $$\left(1-\frac{1}{2022}\right)-\left(1-\frac{2022}{2021}\right): \frac{1}{2021}$$ jest równa
A. 0
B. 1
C. 2021
D. 2023
D
Zadanie 2. [2021 Informator CKE, zad.3, 1 pkt]
Oprocentowanie na długoterminowej lokacie w pewnym banku wynosi $$3 \%$$ w skali roku (już po uwzględnieniu podatków). Po każdym roku oszczędzania są doliczane odsetki od aktualnego kapitału znajdującego się na lokacie - zgodnie z procentem składanym.
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Po 10 latach oszczędzania w tym banku (i bez wypłacania kapitału ani odsetek w tym okresie) kwota na lokacie będzie większa od kwoty wpłaconej na samym początku o (w zaokrągleniu do $$1 \%)$$
A. $$30 \%$$
B. $$34 \%$$
C. $$36 \%$$
D. $$43 \%$$
B
Zadanie 3. [2021 Informator CKE, zad.4, 2 pkt]
Dane są dwie liczby $$x$$ i $$y$$, takie, że iloraz $$\frac{x}{y}$$ jest równy $$\frac{1+\sqrt{5}}{2}$$.
Oblicz wartość wyrażenia $$\frac{x+y}{x}$$. Wynik podaj bez niewymierności w mianowniku.
Sposób 1.
$$
\begin{aligned}
\frac{x+y}{x} &=1+\frac{y}{x}=1+\frac{2}{1+\sqrt{5}}=\frac{1+\sqrt{5}+2}{1+\sqrt{5}}=\frac{3+\sqrt{5}}{1+\sqrt{5}}=\frac{(3+\sqrt{5})(1-\sqrt{5})}{(1+\sqrt{5})(1-\sqrt{5})}=\\
&=\frac{3-3 \sqrt{5}+\sqrt{5}-5}{1-5}=\frac{-2-2 \sqrt{5}}{-4}=\frac{1+\sqrt{5}}{2}
\end{aligned}
$$
Sposób 2.
$$
\begin{aligned}
\frac{x+y}{x} &=1+\frac{y}{x}=1+\frac{2}{1+\sqrt{5}}=1+\frac{2}{(1+\sqrt{5})} \cdot \frac{(1-\sqrt{5})}{(1-\sqrt{5})}=1+\frac{(2-2 \sqrt{5})}{-4}=\\
&=1+\frac{\sqrt{5}-1}{2}=\frac{2+\sqrt{5}-1}{2}=\frac{1+\sqrt{5}}{2}
\end{aligned}
$$
Sposób 3.
$$
\begin{aligned}
\frac{x+y}{x} &=\frac{\frac{x+y}{y}}{\frac{x}{y}}=\frac{\frac{x}{y}+1}{\frac{x}{y}}=\frac{\left(\frac{1+\sqrt{5}}{2}+\frac{2}{2}\right)}{\frac{1+\sqrt{5}}{2}}=\frac{\left(\frac{3+\sqrt{5}}{2}\right)}{\frac{1+\sqrt{5}}{2}}=\frac{3+\sqrt{5}}{1+\sqrt{5}}=\\
&=\frac{(3+\sqrt{5})}{(1+\sqrt{5})} \cdot \frac{(1-\sqrt{5})}{(1-\sqrt{5})}=\frac{-2-2 \sqrt{5}}{-4}=\frac{1+\sqrt{5}}{2}
\end{aligned}
$$
Sposób 4.
Z równości $$\frac{x}{y}=\frac{1+\sqrt{5}}{2}$$ wyznaczamy $$x$$ :
$$
x=\left(\frac{1+\sqrt{5}}{2}\right) y
$$
Wyznaczony $$x$$ podstawimy do wyrażenia $$\frac{x+y}{x}$$ :
$$
\begin{aligned}
\frac{x+y}{x} &=\frac{\left(\frac{1+\sqrt{5}}{2}\right) \cdot y+y}{\left(\frac{1+\sqrt{5}}{2}\right) \cdot y}=\frac{y \cdot\left(\frac{1+\sqrt{5}}{2}+1\right)}{y \cdot\left(\frac{1+\sqrt{5}}{2}\right)}=\frac{\frac{1+\sqrt{5}}{2}+\frac{2}{1+\sqrt{5}}}{\frac{1}{2}}=\frac{\frac{3+\sqrt{5}}{2}}{\frac{1+\sqrt{5}}{2}}=\frac{3+\sqrt{5}}{1+\sqrt{5}}=\\
&=\frac{3+\sqrt{5}}{1+\sqrt{5}}=\frac{(3+\sqrt{5})}{(1+\sqrt{5})} \cdot \frac{(1-\sqrt{5})}{(1-\sqrt{5})}=\frac{-2-2 \sqrt{5}}{-4}=\frac{1+\sqrt{5}}{2}
\end{aligned}
$$
Zadanie 4. [2021 Informator CKE, zad.5, 2 pkt]
Dane są liczby $$a=\sqrt{5}-2$$ oraz $$b=\sqrt{5}+2$$.
Oblicz wartość wyrażenia $$\frac{a \cdot b}{\sqrt{a}+\sqrt{b}}: \frac{\sqrt{a}-\sqrt{b}}{a-b}$$ dla podanych $$a$$ i $$b$$.
Sposób 1.
Przekształcamy równoważnie wyrażenie do najprostszej postaci:
$$
\frac{a \cdot b}{\sqrt{a}+\sqrt{b}}: \frac{\sqrt{a}-\sqrt{b}}{a-b}=\frac{a \cdot b}{\sqrt{a}+\sqrt{b}} \cdot \frac{a-b}{\sqrt{a}-\sqrt{b}}=\frac{a \cdot b(a-b)}{(\sqrt{a})^2-(\sqrt{b})^2}=\frac{a \cdot b(a-b)}{a-b}=a \cdot b
$$
Podstawiamy wartości $$a$$ i $$b$$ do otrzymanego wyrażenia i obliczamy jego wartość:
$$
a \cdot b=(\sqrt{5}-2)(\sqrt{5}+2)=(\sqrt{5})^2-2^2=5-4=1
$$
18 Informator o egzaminie maturalnym z matematyki na poziomie podstawowym od roku szkolnego 2022/2023
Sposób 2.
Zauważmy, że:
$$
a \cdot b=(\sqrt{5}-2) \cdot(\sqrt{5}+2)=(\sqrt{5})^2-2^2=5-4=1
$$
zatem liczby $$a$$ i $$b$$ są wzajemnie odwrotne. Zauważamy także, że:
$$
(\sqrt{a}+\sqrt{b}) \cdot \frac{\sqrt{a}-\sqrt{b}}{a-b}=\frac{a-b}{a-b}=1
$$
co oznacza, że liczby $$\sqrt{a}+\sqrt{b}$$ i $$\frac{\sqrt{a}-\sqrt{b}}{a-b}$$ także są wzajemnie odwrotne: $$\frac{\sqrt{a}-\sqrt{b}}{a-b}=\frac{1}{\sqrt{a}+\sqrt{b}}$$
Z powyższych zależności wynika:
$$
\frac{a \cdot b}{\sqrt{a}+\sqrt{b}}: \frac{\sqrt{a}-\sqrt{b}}{a-b}=a b \cdot \frac{1}{\sqrt{a}+\sqrt{b}}: \frac{1}{\sqrt{a}+\sqrt{b}}=1 \cdot 1=1
$$
Zadanie 5. [2021 Informator CKE, zad.6, 2 pkt]
Dana jest liczba $$x=a-(\sqrt{3}-\sqrt{2})^2$$, gdzie $$a$$ należy do zbioru $$\mathbb{R}$$ liczb rzeczywistych. W rozwiązaniu zadania uwzględnij fakt, że liczby $$\sqrt{3}$$ oraz $$\sqrt{2} \cdot \sqrt{3}$$ są niewymierne.
Dokończ zdanie. Zaznacz dwie odpowiedzi, tak aby dla każdej z nich dokończenie zdania było prawdziwe.
Liczba $$x$$ jest wymierna dla
A. $$a=5$$
B. $$a=-\sqrt{3}+\sqrt{2}$$
C. $$a=(\sqrt{2}-\sqrt{3})^2+0,3$$
D. $$a=6$$
E. $$a=-2 \sqrt{6}+12,5$$
F. $$a=(\sqrt{2}-\sqrt{3})^2-2 \sqrt{6}$$
G. $$a=-\sqrt{6}$$
CE
Komentarz
Przekształcimy równoważnie wyrażenie określające liczbę $$x-\mathrm{w}$$ tym celu zastosujemy m.in. Wzór skróconego mnożenia:
$$
\begin{aligned}
x &=a-(\sqrt{3}-\sqrt{2})^2=a-\left(\sqrt{3}^2-2 \cdot \sqrt{3} \cdot \sqrt{2}+\sqrt{2}^2\right)=a-(3-2 \sqrt{6}+2) \\
&=a-(5-2 \sqrt{6})=a-5+2 \sqrt{6}
\end{aligned}
$$
Liczba $$x$$ będzie wymierna, jeśli liczba $$a$$ będzie postaci: $$a=q-2 \sqrt{6}$$, gdzie $$q$$ będzie dowolną liczbą wymierną:
$$
x=q-2 \sqrt{6}-5+2 \sqrt{6}=q-5
$$
Sprawdzimy, które z liczb $$a$$ podanych w odpowiedziach A-G mają postać $$a=q-2 \sqrt{6}$$ (gdzie $$q$$ jest wymierne):
A. $$a=5$$
B. $$a=-\sqrt{3}+\sqrt{2}$$
C. $$a=(\sqrt{2}-\sqrt{3})^2+0,3=5-2 \sqrt{6}+0,3=5,3-2 \sqrt{6}$$
D. $$a=6$$
E. $$a=-2 \sqrt{6}+12,5$$
F. $$a=5-2 \sqrt{6}-2 \sqrt{6}=5-4 \sqrt{6}$$
G. $$a=-\sqrt{6}$$
Liczby podane w odpowiedziach C i E mają żądaną postać.
Zadanie 6. [2021 Informator CKE, zad.8, 2 pkt]
Pensja pana X jest o $$50 \%$$ wyższa od średniej krajowej, a pensja pana Y jest o $$40 \%$$ niższa od średniej krajowej.
Dokończ zdania. Zaznacz odpowiedź spośród A-D oraz odpowiedź spośród E-H.
1. Pensja pana $$X$$ jest wyższa od pensji pana $$Y$$
A. o $$40 \%$$ pensji pana $$Y$$.
B. o $$90 \%$$ pensji pana $$Y$$.
C. o $$150 \%$$ pensji pana $$Y$$.
D. o $$275 \%$$ pensji pana $$\mathrm{Y}$$.
2. Pensja pana $$Y$$ jest niższa od pensji pana $$X$$
E. o $$60 \%$$ pensji pana $$X$$.
F. o $$73 \%$$ pensji pana $$X$$.
G. o $$90 \%$$ pensji pana $$X$$.
H. o $$150 \%$$ pensji pana X.
1.C $$2 . E$$
Komentarz
Średnią krajową oznaczymy jako $$s$$, pensję pana $$\mathrm{X}$$ jako $$x$$, a pensję pana $$\mathrm{Y}$$ jako $$y$$.
Wtedy: $$x=1,5 s \quad y=0,6 s$$. Wykonujemy obliczenia:
$$
\frac{x}{y}=\frac{1,5 s}{0,6 s}=2,5(250 \%=100 \%+150 \%) \quad \frac{y}{x}=\frac{0,6 s}{1,5 s}=0,4(40 \%=100 \%-60 \%)
$$
Zadanie 7. [2021 Informator CKE, zad.9, 1 pkt]
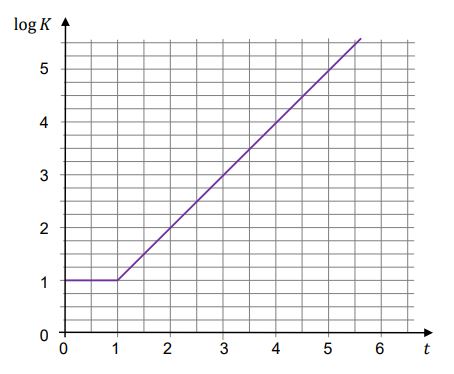
Na wykresie przedstawiono zależność $$\log K(t)$$, gdzie $$K(t)$$ jest liczbą bakterii w próbce po czasie $$t$$ wyrażonym w godzinach, jaki upłynął od chwili $$t=0$$ rozpoczęcia obserwacji.
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Gdy upłynęły dokładnie trzy godziny od chwili $$t=0$$, liczba $$K$$ bakterii była równa
A. 3
B. 100
C. 1000
D. 10000
C
Zadanie 8. [2021 Informator CKE, zad.10, 1 pkt]
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Liczba $$\log _2\left[(\sqrt{2})^2 \cdot(\sqrt{2})^4 \cdot(\sqrt{2})^8\right]$$ jest równa
A. $$\sqrt{2}$$
B. 7
C. 14
D. $$2^7$$
B
Zadanie 9. [2021 Informator CKE, zad.10, 1 pkt]
Rozważmy takie liczby rzeczywiste $$a$$ i $$b$$, które spełniają warunki:
$$
a \neq 0, b \neq 0 \text { oraz } a^3+b^3=(a+b)^3 .
$$
Oblicz wartość liczbową wyrażenia $$\frac{a}{b}$$ dla dowolnych liczb rzeczywistych $$a$$ i $$b$$, spełniających powyższe warunki.
Sposób 1.
Równanie podane w zadaniu przekształcamy w sposób równoważny. Do prawej strony równania zastosujemy wzór na trzecią potęgę sumy liczb $$a$$ i $$b$$ :
$$
\begin{aligned}
&a^3+b^3=(a+b)^3 \\
&a^3+b^3=a^3+3 a^2 b+3 a b^2+b^3 \\
&0=3 a^2 b+3 a b^2 \\
&3 a b(a+b)=0
\end{aligned}
$$
lloczyn po lewej stronie równania jest równy 0 , gdy co najmniej jeden z czynników jest równy 0.
Zatem:
$$
3 a b=0 \quad \text { lub } \quad a+b=0
$$
Stąd mamy:
$$
a=0 \text { lub } b=0 \text { lub } a=-b
$$
Gdy uwzględnimy warunki zadania $$a \neq 0$$ i $$b \neq 0$$, to otrzymujemy:
$$
\frac{a}{b}=\frac{-b}{b}=-1
$$
Sposób 2.
Przekształcamy równanie w sposób równoważny:
$$
\begin{aligned}
&a^3+b^3=(a+b)^3 \\
&a^3+b^3-(a+b)^3=0 \\
&a^3+\left[b^3-(a+b)^3\right]=0
\end{aligned}
$$
Do wyrażenia w nawiasie kwadratowym zastosujemy wzór na różnicę sześcianów:
$$
\begin{aligned}
&a^3+[b-(a+b)] \cdot\left[b^2+b \cdot(a+b)+(a+b)^2\right]=0 \\
&a^3+(-a) \cdot\left(b^2+a b+b^2+a^2+2 a b+b^2\right)=0 \\
&a^3+(-a) \cdot\left(a^2+3 a b+3 b^2\right)=0 \\
&a^3-a^3-3 a^2 b-3 a b^2=0 \\
&-3 a b(a+b)=0
\end{aligned}
$$
Ponieważ $$a \neq 0$$ i $$b \neq 0$$, to powyższe równanie jest spelnione gdy:
$$
a+b=0
$$
Zatem:
$$
a=-b \quad \text { stąd otrzymujemy } \quad \frac{a}{b}=-1
$$
Zadanie 10. [2022 marzec, zad.1, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wartość wyrażenia $$6^{100}+6^{100}+6^{100}+6^{100}+6^{100}+6^{100}$$ jest równa
A. $$6^{600}$$
B. $$6^{101}$$
C. $$36^{100}$$
D. $$36^{600}$$
B
Zadanie 11. [2022 marzec, zad.2, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wartość wyrażenia $$\log _7 98-\log _7 2$$ jest równa
A. 7
B. 2
C. 1
D. (-1)
B
Zadanie 12. [2022 marzec, zad.4, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dla każdej liczby rzeczywistej $$a$$ wartość wyrażenia $$(3+4 a)^2-(3-4 a)^2$$ jest równa
A. $$32 a^2$$
B. 0
C. $$48 a$$
D. $$8 a^2$$
B
Zadanie 13. [2022 wrzesień, zad.1, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wartość wyrażenia $$\left(1+3 \cdot 2^{-1}\right)^{-2}$$ jest równa
A. $$\frac{25}{4}$$
B. $$\frac{4}{25}$$
C. $$\frac{36}{49}$$
D. $$\frac{40}{9}$$
B
Komentarz
Obliczamy wartość wyrażenia:
$$
\left(1+3 \cdot 2^{-1}\right)^{-2}=\left(1+3 \cdot \frac{1}{2}\right)^{-2}=\left(1+\frac{3}{2}\right)^{-2}=\left(\frac{5}{2}\right)^{-2}=\left(\frac{2}{5}\right)^2=\frac{4}{25}
$$
Zadanie 14. [2022 wrzesień, zad.2, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wartość wyrażenia $$2 \log _5 5+1-\frac{1}{2} \log _5 625$$ jest równa
A. 1
B. 5
C. 10
D. 25
A
Komentarz
Obliczamy wartość wyrażenia:
$$
2 \log _5 5+1-\frac{1}{2} \log _5 625=2 \cdot 1+1-\frac{1}{2} \cdot 4=2+1-2=1
$$
Zadanie 15. [2022 wrzesień, zad.5, 2 pkt]
Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Dla każdej liczby rzeczywistej $$x$$ i dla każdej liczby rzeczywistej $$y$$ myrażenie $$9-\left(x^2-2 x y+y^2\right)$$ jest równe
A. $$[3-(x-2 y)]^2$$
B. $$[3+(x-2 y)]^2$$
C. $$[3-(x+2 y)]^2$$
D. $$[3-(x-y)] \cdot[3+(x-y)]$$
E. $$[3-(x+2 y)] \cdot[3+(x+2 y)]$$
F. $$-[(x-y)-3] \cdot[(x-y)+3]$$
D F
Komentarz
Przekształcamy wyrażenia, stosując wzór skróconego mnożenia na różnicę kwadratów dwóch wyrażeń:
$$
[3-(x-y)] \cdot[3+(x-y)]=9-(x-y)^2=9-\left(x^2-2 x y+y^2\right)
$$
oraz
$$
-[(x-y)-3] \cdot[(x-y)+3]=-\left[(x-y)^2-9\right]=9-\left(x^2-2 x y+y^2\right)
$$
Zadanie 16. [2022 marzec, zad.14, 1 pkt]
Klient wpłacił do banku 20000 zł na lokatę dwuletnią. Po każdym rocznym okresie oszczędzania bank dolicza odsetki w wysokości $$3 \%$$ od kwoty bieżącego kapitalu znajdującego się na lokacie.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Po 2 latach oszczędzania w tym banku kwota na lokacie (bez uwzględniania podatków) jest równa
A. $$20000 \cdot(1,12)^2$$
B. $$20000 \cdot 2 \cdot 1,03$$
C. $$20000 \cdot 1,06$$
D. $$20000 \cdot(1,03)^2$$
D
Zadanie 17. [2022 Zbiór zadań CKE, zad.2, 1 pkt]
Liczbę $$a=(\sqrt{2}+\sqrt{7})^2$$ można zapisać w postaci $$a=x+y \sqrt{14}$$, gdzie $$x \in \mathbb{Z}$$ oraz $$y \in \mathbb{Z}$$.
Uzupełnij poniższe równości. Wpisz właściwe liczby w wykropkowanych miejscach.
$$
\begin{aligned}
&x=..... \\
&y=.....
\end{aligned}
$$
$$x=9$$
$$y=2$$
Zadanie 18. [2022 Zbiór zadań CKE, zad.3, 3 pkt]
Rozważmy takie liczby rzeczywiste $$a$$ i $$b$$, które spełniają warunki:
$$
a \neq 0 \quad \text { oraz } b \neq 0 \quad \text { oraz } \quad a \sqrt{2}+b \sqrt{3}=0
$$
Oblicz wartość liczbową wyrażenia $$\frac{a}{b}+\frac{b}{a}$$ dla dowolnych liczb rzeczywistych $$a$$ i $$b$$, spełniających powyższe warunki. Wynik podaj w postaci ułamka bez niewymierności w mianowniku.
Z warunków zadania mamy
$$
a \sqrt{2}+b \sqrt{3}=0
$$
Wynika stąd, że
$$
a \sqrt{2}=-b \sqrt{3}
$$
Mamy zatem zależność
$$
\frac{a}{b}=-\frac{\sqrt{3}}{\sqrt{2}} \text { oraz } \frac{b}{a}=-\frac{\sqrt{2}}{\sqrt{3}}
$$
Podstawiając te wartości do wyrażenia $$\frac{a}{b}+\frac{b}{a}$$ mamy:
$$
\frac{a}{b}+\frac{b}{a}=-\frac{\sqrt{2}}{\sqrt{3}}-\frac{\sqrt{3}}{\sqrt{2}}=-\frac{\sqrt{6}}{3}-\frac{\sqrt{6}}{2}=-\frac{2 \sqrt{6}}{6}-\frac{3 \sqrt{6}}{6}=-\frac{5 \sqrt{6}}{6}
$$
Zadanie 19. [2022 Zbiór zadań CKE, zad.5, 1 pkt]
Która z podanych równości (A-D) jest prawdziwa? Wybierz właściwą odpowiedź spośród podanych.
A. $$(\sqrt{7}+\sqrt{5})^3=\sqrt{7^3}+\sqrt{5^3}$$
B. $$\sqrt{\sqrt{144}+\sqrt{16}}=2^{\frac{4}{2}}$$
c. $$\left(\sqrt{2 \frac{1}{4}}\right)^3=2^{\frac{3}{2}}+\left(\frac{1}{2}\right)^3$$
D. $$(\sqrt[3]{64})^{\frac{1}{8}}=8^3$$
B
Komentarz
Stosując związek pierwiastkowania z potęgowaniem oraz prawa działań na potęgach i pierwiastkach otrzymujemy:
$$
\sqrt{\sqrt{144}+\sqrt{16}}=\sqrt{12+4}=\sqrt{16}=4=2^2=2^{\frac{4}{2}}
$$
Zadanie 20. [2022 Zbiór zadań CKE, zad.7, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wartość wyrażenia $$\log k+\log \frac{1}{100} k^2-\log \frac{1}{10} k^3$$, gdzie $$k>0$$, jest równa
A. $$0$$
B. $$1$$
C. $$(-1)$$
D. $$k$$
C
Komentarz
Stosując wzór na logarytm iloczynu oraz logarytm potęgi, otrzymujemy przekształcanie:
$$
\begin{gathered}
\log k+\log \frac{1}{100} k^2-\log \frac{1}{10} k^3=\log k+\log \frac{1}{100}+\log k^2-\left(\log \frac{1}{10}+\log k^3\right)= \\
=\log k-2+2 \log k+1-3 \log k=-1
\end{gathered}
$$
Zadanie 21. [2022 Zbiór zadań CKE, zad.8, 2 pkt]
Liczby rzeczywiste $$x, y, z$$ spełniają następujące warunki:
$$
x, y, z>0 \text { oraz } x, y, z \neq 1 \text { oraz } y^z=x
$$
Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Z podanych warunków wynika, że prawdziwe są równości
A. $$\log _x y=z$$
B. $$y^{-\log _y x}=\frac{1}{x}$$
C. $$\log _x z=y$$
D. $$y^{\log _x y}=x$$
E. $$\log _y x=z$$
F. $$z^{-\log _x z}=\frac{1}{y}$$
B E
Zadanie 22. [2022 Zbiór zadań CKE, zad.9, 1 pkt]
Oceń prawdziwość poniższych stwierdzeń. Wybierz $$P$$, jeśli stwierdzenie jest prawdziwe, albo $$\mathrm{F}$$ - jeśli jest fałszywe.
$$
\begin{array}{|l|l|l|}
\hline \begin{array}{l}
\text { Wyrażenie } 2 x^2-1 \text { można przekształcić równoważnie do wyrażenia } \\
(1-x \sqrt{2})(x \sqrt{2}-1) .
\end{array} & \mathbf{P} & \mathbf{F} \\
\hline \begin{array}{l}
\text { Dla każdej liczby rzeczywistej } x \text { wartość wyrażenia } \\
(2+x)^3-x^2(x+6)-12 x \text { jest równa } 8 .
\end{array} & \mathbf{P} & \mathbf{F} \\
\hline
\end{array}
$$
F P
Zadanie 23. [2022 grudzień, zad.1, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba $$\left(5 \cdot 5^{\frac{1}{2}}\right)^{\frac{1}{3}}$$ jest równa
A. $$\sqrt[6]{5}$$
B. $$\sqrt[3]{25}$$
C. $$\sqrt{5}$$
D. $$\sqrt[3]{5}$$
C
Zadanie 24. [2022 grudzień, zad.2, 1 pkt]
Pan Nowak kupił obligacje Skarbu Państwa za 40000 zł oprocentowane $$7 \%$$ w skali roku. Odsetki są naliczane i kapitalizowane co rok.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wartość obligacji kupionych przez pana Nowaka będzie po dwóch latach równa
A. $$40000 \cdot(1,07)^2$$ zł
B. $$40000 \cdot(1,7)^2$$ zł
C. $$40000 \cdot 1,14$$ zł
D. $$40000 \cdot 1,49$$ zł
A
Zadanie 25. [2022 grudzień, zad.4, 1 pkt]
Liczby rzeczywiste $$x$$ i $$y$$ są dodatnie oraz $$x \neq y$$
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wyrażenie $$\frac{1}{x-y}+\frac{1}{x+y}$$ można przekształcić do postaci
A. $$\frac{2}{x-y}$$
B. $$\frac{2}{x^2-y^2}$$
C. $$\frac{2 x}{x^2-y^2}$$
D. $$\frac{-2 x y}{x+y}$$
C
Zadanie 26. [2023 maj, zad.2, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba $$\sqrt[3]{-\frac{27}{16}} \cdot \sqrt[3]{2}$$ jest równa
A. $$\left(-\frac{3}{2}\right)$$
B. $$\frac{3}{2}$$
C. $$\frac{2}{3}$$
D. $$\left(-\frac{2}{3}\right)$$
A
Zadanie 27. [2023 maj, zad.4, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba $$\log _9 27+\log _9 3$$ jest równa
A. 81
B. 9
C. 4
D. 2
D
Zadanie 28. [2023 czerwiec, zad.2, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dla każdej dodatniej liczby rzeczywistej $$x$$ iloczyn $$\sqrt{x} \cdot \sqrt[3]{x} \cdot \sqrt[6]{x}$$ jest równy
A. $$x$$
B. $$\sqrt[10]{x}$$
C. $$\sqrt[18]{x}$$
D. $$x^2$$
A
Zadanie 29. [2023 czerwiec, zad.4, 1 pkt]
Klient wpłacił do banku 30000 zł na lokatę dwuletnią. Po każdym rocznym okresie oszczędzania bank dolicza odsetki w wysokości $$7 \%$$ od kwoty bieżącego kapitału znajdującego się na lokacie.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Po dwóch latach oszczędzania łączna wartość doliczonych odsetek na tej lokacie (bez uwzględniania podatków) jest równa
A. $$2100 \mathrm{zł}$$
B. 2247 zł
C. $$4200 \mathrm{z}$$ 가
D. $$4347 \mathrm{z}$$ 각
D
Zadanie 30. [2023 czerwiec, zad.5, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba $$\log _2 \frac{1}{8}+\log _2 4$$ jest równa
A. $$(-1)$$
B. $$\frac{1}{2}$$
C. 2
D. 5
A
Zadanie 31. [2023 czerwiec, zad.6, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba $$(1+\sqrt{5})^2-(1-\sqrt{5})^2$$ jest równa
A. 0
B. $$(-10)$$
C. $$4 \sqrt{5}$$
D. $$2+2 \sqrt{5}$$
C
Zadanie 32. [2023 sierpień, zad.2, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(3 \sqrt{45}-\sqrt{20}\) jest równa
A. \((7 \cdot 5)^{\frac{1}{2}}\)
B. \(5^{\frac{1}{2}}\)
C. 7
D. \(7 \cdot 5^{\frac{1}{2}}\)
D
Zadanie 33. [2023 sierpień, zad.3, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\log _{25} 1-\frac{1}{2} \log _{25} 5\) jest równa
A. \(\left(-\frac{1}{4}\right)\)
B. \(\left(-\frac{1}{2}\right)\)
C. \(\frac{1}{4}\)
D. \(\frac{1}{2}\)
A
Zadanie 34. [2023 sierpień, zad.5, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wartość wyrażenia \(\frac{3^{-1}}{\left(-\frac{1}{9}\right)^{-2}} \cdot 81\) jest równa
A. \(\frac{1}{3}\)
B. \(\left(-\frac{1}{3}\right)\)
C. 3
D. \((-3)\)
A
Zadanie 35. [2023 sierpień, zad.6, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wartość wyrażenia \((2-\sqrt{3})^2-(\sqrt{3}-2)^2\) jest równa
A. \((-2 \sqrt{3})\)
B. 0
C. 6
D. \(8 \sqrt{3}\)
B
Zadanie 36. [2023 grudzień, zad.1, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\left(3^{-2,4} \cdot 3^{\frac{2}{5}}\right)^{\frac{1}{2}}\) jest równa
A. \(\sqrt{3}\)
B. \(\frac{\sqrt{3}}{3}\)
C. \(\frac{1}{3}\)
D. 0,3
C
Zadanie 37. [2023 grudzień, zad.2, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\log _{2} 96-\log _{2} 3\) jest równa
A. \(\log _{2} 93\)
B. \(\log _{2} 30\)
C. 4
D. 5
D
Zadanie 38. [2023 grudzień, zad.3, 1 pkt]
Pan Grzegorz wpłacił do banku pewną kwotę na lokatę dwuletnią. Po każdym rocznym okresie oszczędzania bank doliczał odsetki w wysokości \(5 \%\) od kwoty bieżącego kapitału znajdującego się na lokacie. Po dwóch latach oszczędzania pan Grzegorz odebrał z tego banku wraz z odsetkami kwotę 4851 zł (bez uwzględnienia podatków).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Kwota wpłacona przez pana Grzegorza na tę lokatę była równa
A. 4300 zł
B. 4400 zł
C. 4500 zł
D. 4600 zł
B
Zadanie 39. [2023 grudzień, zad.12, 1 pkt]
Proces stygnięcia naparu z ziół w otoczeniu o stałej temperaturze \(22^{\circ} \mathrm{C}\) opisuje funkcja wykładnicza \(T(x)=78 \cdot 2^{-0,05 x}+22\), gdzie \(T(x)\) to temperatura naparu wyrażona w stopniach Celsjusza \(\left({ }^{\circ} \mathrm{C}\right)\) po \(x\) minutach liczonych od momentu \(x=0\), w którym zioła zalano wrzątkiem.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Temperatura naparu po 20 minutach od momentu zalania ziół wrzątkiem jest równa
A. \(22^{\circ} \mathrm{C}\)
B. \(39^{\circ} \mathrm{C}\)
C. \(78^{\circ} \mathrm{C}\)
D. \(61^{\circ} \mathrm{C}\)
D
Zadanie 40. [2024 maj, zad.2, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\left(\frac{1}{16}\right)^{8} \cdot 8^{16}\) jest równa
A. \(2^{24}\)
B. \(2^{16}\)
C. \(2^{12}\)
D. \(2^{8}\)
B
Zadanie 41. [2024 maj, zad.4, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\log _{\sqrt{3}} 9\) jest równa
A. 2
B. 3
C. 4
D. 9
C
Zadanie 42. [2024 maj, zad.5, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dla każdej liczby rzeczywistej \(a\) i dla każdej liczby rzeczywistej \(b\) wartość wyrażenia \((2 a+b)^{2}-(2 a-b)^{2}\) jest równa wartości wyrażenia
A. \(8 a^{2}\)
B. \(8 a b\)
C. \(-8 a b\)
D. \(2 b^{2}\)
B
Zadanie 43. [2024 maj, zad.6, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Zbiorem wszystkich rozwiązań nierówności
\[1-\frac{3}{2} x<\frac{2}{3}-x\]
jest przedział
A. \(\left(-\infty,-\frac{2}{3}\right)\)
B. \(\left(-\infty, \frac{2}{3}\right)\)
C. \(\left(-\frac{2}{3},+\infty\right)\)
D. \(\left(\frac{2}{3},+\infty\right)\)
D
Zadanie 44. [2024 maj, zad.7, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Równanie \(\frac{x+1}{(x+2)(x-3)}=0 \mathrm{w}\) zbiorze liczb rzeczywistych
A. nie ma rozwiązania.
B. ma dokładnie jedno rozwiązanie: \((-1)\).
C. ma dokładnie dwa rozwiązania: \((-2)\) oraz 3 .
D. ma dokładnie trzy rozwiązania: \((-1),(-2)\) oraz 3 .
B
Zadanie 45. [2024 czerwiec, zad.1, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(2^{-1} \cdot 32^{\frac{3}{5}}\) jest równa
A. \((-16)\)
B. \((-4)\)
C. 2
D. 4
D
Zadanie 46. [2024 czerwiec, zad.2, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\log _{3}\left(\frac{3}{2}\right)+\log _{3}\left(\frac{2}{9}\right)\) jest równa
A. \(\log _{3} \frac{31}{18}\)
B. \(\log _{3} \frac{5}{11}\)
C. \((-1)\)
D. \(\frac{1}{3}\)
C
Zadanie 47. [2024 czerwiec, zad.3, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \((2 \sqrt{10}+\sqrt{2})^{2}\) jest równa
A. 22
B. 42
C. \(42+4 \sqrt{5}\)
D. \(42+8 \sqrt{5}\)
D
Zadanie 48. [2024 czerwiec, zad.4, 1 pkt]
Klient wpłacił do banku na trzyletnią lokatę kwotę w wysokości \(K_{0}\) zł. Po każdym rocznym okresie oszczędzania bank dolicza odsetki w wysokości \(6 \%\) od kwoty bieżącego kapitału znajdującego się na lokacie - zgodnie z procentem składanym.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Po trzech latach oszczędzania w tym banku kwota na lokacie (bez uwzględniania podatków) jest równa
A. \(K_{0} \cdot(1,06)^{3}\)
B. \(K_{0} \cdot(1,02)^{3}\)
C. \(K_{0} \cdot(1,03)^{6}\)
D. \(K_{0} \cdot 1,18\)
A
Zadanie 49. [2024 grudzień, zad.1, 1 pkt]
Liczby \(x_{1}\) i \(x_{2}\) są różnymi rozwiązaniami równania \(|x+4|=7\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Suma \(x_{1}+x_{2}\) jest równa
A. \((-14)\)
B. \((-8)\)
C. 3
D. 8
B
Zadanie 50. [2024 grudzień, zad.2, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\left(\sqrt[5]{5} \cdot \frac{1}{5}\right)^{-5}\) jest równa
A. \(5^{4}\)
B. \(5^{-4}\)
C. \(5^{0,25}\)
D. \(5^{-0,25}\)
A
Zadanie 51. [2024 grudzień, zad.4, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dla każdej dodatniej liczby rzeczywistej \(x\) i dla każdej dodatniej liczby rzeczywistej \(y\) wartość wyrażenia \(\log _{7} x+6 \log _{7} y\) jest równa wartości wyrażenia
A. \(\log _{7}\left(\frac{x}{y^{6}}\right)\)
B. \(\log _{7}(x y)^{6}\)
C. \(\log _{7}(6 x y)\)
D. \(\log _{7}\left(x y^{6}\right)\)
D
Zadanie 52. [2024 grudzień, zad.5, 1 pkt]
Pani Aniela wpłaciła do banku kwotę 60000 zł na lokatę dwuletnią. Po każdym rocznym okresie oszczędzania bank doliczał odsetki w wysokości \(p \%\) w skali roku od kwoty bieżącego kapitału znajdującego się na lokacie - zgodnie z procentem składanym. Na koniec okresu oszczędzania kwota na tej lokacie była równa 67925,76 zł wraz z odsetkami (bez uwzględniania podatków).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Oprocentowanie lokaty w skali roku było równe
A. \(6 \%\)
B. \(6,4 \%\)
C. \(6,5 \%\)
D. \(7 \%\)
B
Zadanie 53. [2024 sierpień, zad.2, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\left(\frac{4}{25}\right)^{-0,5}\) jest równa
A. 0,04
B. 0,8
C. 2,5
D. 0,4
C
Zadanie 54. [2024 sierpień, zad4, 2 pkt]
Uzupełnij zdanie. Wybierz dwie właściwe odpowiedzi spośród oznaczonych literami A-F i wpisz te litery w wykropkowanych miejscach.
Prawdziwe są równości: \(\qquad\) oraz \(\qquad\)
A. \(\log _2 16+\log _2 9=\log _2 25\)
B. \(\log _2 16+\log _2 9=2 \cdot \log _2 5\)
C. \(\log _2 16+\log _2 9=\log _2 144\)
D. \(\log _2 16+\log _2 9=\log _4 144\)
E. \(\log _2 16+\log _2 9=4+2 \cdot \log _2 3\)
F. \(\log _2 16+\log _2 9=2 \cdot \log _4 12\)
C E
Zadanie 55. [2024 sierpień SF, zad. 1, 1 pkt]

A
Zadanie 56. [2024 sierpień SF, zad. 4, 1 pkt]

A
Zadanie 57. [2025 maj, zad. 1, 1 pkt]
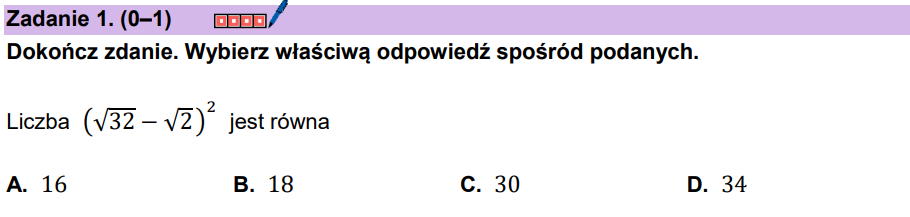
B
Zadanie 58. [2025 maj, zad. 2, 1 pkt]

B
Zadanie 59. [2025 maj, zad. 3, 1 pkt]
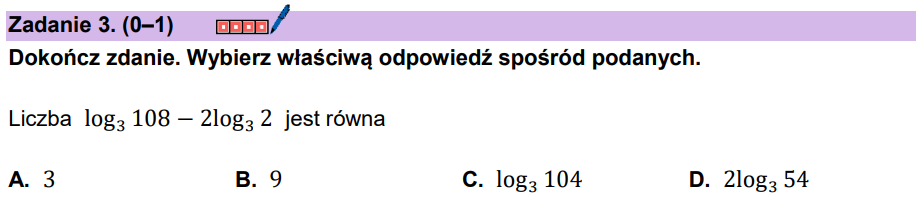
A
Zadanie 60. [2025 czerwiec, zad. 2, 1 pkt]
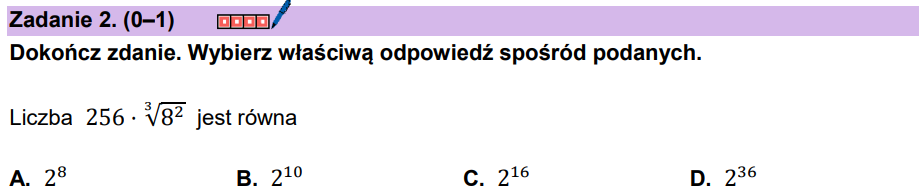
B
Zadanie 61. [2025 czerwiec, zad. 3, 1 pkt]

PF
Zadanie 62. [2025 czerwiec, zad. 4, 1 pkt]

D
Zadanie 63. [2025 sierpień, zad. 1, 1 pkt]

C
Zadanie 64. [2025 sierpień, zad. 2, 1 pkt]
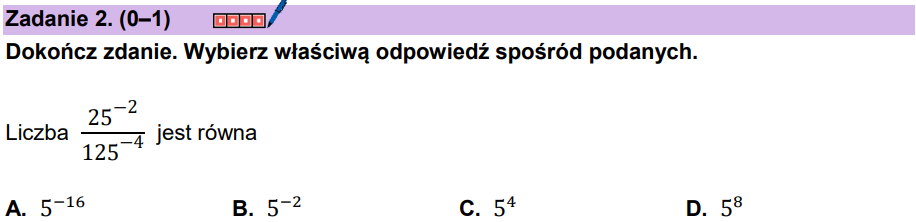
D
Zadanie 65. [2025 sierpień, zad. 3, 1 pkt]
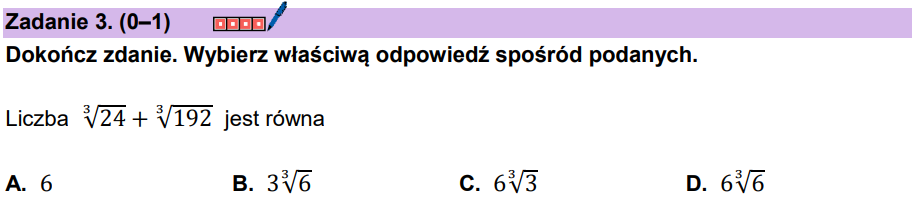
C
Zadanie 66. [2025 sierpień, zad. 4, 1 pkt]

A