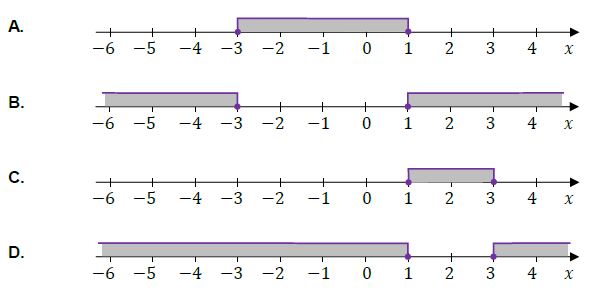
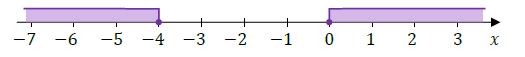Zadanie 1. [2021 Informator CKE, zad.2, 1 pkt]
Dana jest nierówność:
$$
|x-3| \geq 5
$$
Na którym rysunku prawidłowo zaznaczono na osi liczbowej zbiór wszystkich liczb spełniających powyższą nierówność? Zaznacz właściwą odpowiedź spośród podanych.
A
Zadanie 2. [2021 Informator CKE, zad.7, 2 pkt]
Rozwiąż równanie:
$$
\frac{(4 x+1)(x-5)}{(2 x-10)(x+3)}=0
$$
Sposób 1.
Rozwiązaniami równania postaci $$\frac{V(x)}{W(x)}=0$$ są takie liczby $$x_i$$, dla których:
$$
V\left(x_i\right)=0 \quad \text { oraz } \quad W\left(x_i\right) \neq 0
$$
Mianownik ułamka $$\frac{(4 x+1)(x-5)}{(2 x-10)(x+3)}$$ musi być różny od zera, zatem:
$$
(2 x-10)(x+3) \neq 0
$$
lloczyn jest różny od zera, gdy każdy z czynników iloczynu jest różnym od zera:
$$
\begin{array}{lll}
2 x-10 \neq 0 & \text { oraz } & x+3 \neq 0 \\
x \neq 5 & \text { oraz } & x \neq-3
\end{array}
$$
Gdy mianownik ułamka jest różny od zera, to ułamek jest wtedy równy zero, gdy licznik jest równy zero, zatem:
$$
(4 x+1)(x-5)=0
$$
lloczyn jest równy zero, gdy co najmniej jeden z jego czynników jest równy zero:
$$
\begin{array}{lll}
4 x+1=0 & \text { lub } & x-5=0 \\
x=-\frac{1}{4} & \text { lub } & x=5
\end{array}
$$
Ponieważ $$x \neq 5$$, to rozwiązaniem równania jest liczba $$x=-\frac{1}{4}$$.
Sposób 2.
Wyrażenie po lewej stronie równania $$\frac{(4 x+1)(x-5)}{(2 x-10)(x+3)}=0$$ ma sens liczbowy, gdy:
$$
\begin{aligned}
&(2 x-10)(x+3) \neq 0 \\
&x \neq 5 \quad \text { oraz } \quad x \neq-3
\end{aligned}
$$
Zatem równanie $$\frac{(4 x+1)(x-5)}{(2 x-10)(x+3)}=0$$ jest określone dla $$x \in \mathbb{R} \backslash\{5,-3\}$$. Przekształcimy równoważnie równanie:
$$
\begin{aligned}
&\frac{(4 x+1)(x-5)}{(2 x-10)(x+3)}=0 \\
&\frac{(4 x+1)(x-5)}{2(x-5)(x+3)}=0 \\
&\frac{4 x+1}{2(x+3)}=0
\end{aligned}
$$
Gdy mianownik ułamka jest różny od zera, to ułamek jest wtedy równy zero, gdy licznik jest równy zero, zatem:
$$
\begin{aligned}
&4 x+1=0 \\
&x=-\frac{1}{4}
\end{aligned}
$$
Zadanie 3. [2021 Informator CKE, zad.13, 3 pkt]
Rozwiąż równanie
$$
\text { }(x-1)^4-5(x-1)^2+6=0 \text {. }
$$
Zauważmy, że równanie w tym zadaniu jest przykładem równania dwukwadratowego. Dlatego w równaniu $$(x-1)^4-5(x-1)^2+6=0$$ podstawiamy $$z=(x-1)^2$$, gdzie $$z \geq 0$$, po czym otrzymujemy równanie kwadratowe $$z$$ niewiadomą $$z$$ :
$$
z^2-5 z+6=0 \quad z=(x-1)^2 \quad \text { gdzie } \quad z \geq 0
$$
Sposób 1, rozwiązania równania $$z^2-5 z+6=0$$
Rozwiążemy równanie kwadratowe wykorzystując metodę dopełnienia wyrażenia do pełnego kwadratu. Przekształcimy równoważnie trójmian kwadratowy po lewej stronie równania:
$$
\begin{aligned}
\left(z^2-5 z\right)+6 &=\left[z^2-2 \cdot \frac{5}{2} z+\left(\frac{5}{2}\right)^2-\left(\frac{5}{2}\right)^2\right]+6=\left(z-\frac{5}{2}\right)^2-\frac{25}{4}+6=\\
&=\left(z-\frac{5}{2}\right)^2-\frac{1}{4}
\end{aligned}
$$
Rozwiążemy równanie po przekształceniu równoważnym:
$$\left(z-\frac{5}{2}\right)^2-\frac{1}{4}$$
$$\left|z-\frac{5}{2}\right|=\frac{1}{2}$$
$$z-\frac{5}{2}=\frac{1}{2} \quad$$ lub $$\quad z-\frac{5}{2}=-\frac{1}{2}$$
$$z=3 \quad$$ lub $$\quad z=2$$
Sposób 2. rozwiązania równania $$z^2-5 z+6=0$$
Obliczymy tzw. wyróżnik równania kwadratowego (zobacz w Wybranych wzorach matematycznych):
$$
\Delta_z=b^2-4 a c=(-5)^2-4 \cdot 1 \cdot 6=1 .
$$
Ponieważ $$\Delta_z>0$$ to możemy zastosować gotowe wzory (podane w Wybranych wzorach matematycznych) na rozwiązania równania kwadratowego:
$$
z_1=\frac{-b-\sqrt{\Delta_z}}{2 a} \quad z_2=\frac{-b+\sqrt{\Delta_z}}{2 a}
$$
Rozwiązania równania kwadratowego:
$$
z_1=2 \quad \text { lub } \quad z_2=3
$$
Powracamy do podstawienia $$z=(x-1)^2$$ i wyznaczamy rozwiązania równania podanego w zadaniu:
$$\begin{array}{lll}(x-1)^2=2 & \text { lub } & (x-1)^2=3 \\ |x-1|=\sqrt{2} & \text { lub } & |x-1|=\sqrt{3}\end{array}$$
Stąd: $$x_{11}=\sqrt{2}+1$$ lub $$x_{12}=-\sqrt{2}+1$$ lub $$\quad x_{21}=\sqrt{3}+1$$ lub $$x_{22}=-\sqrt{3}+1$$
Zadanie 4. [2022 marzec, zad.7, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Równanie
$$
\frac{(4 x-6)(x-2)^2}{2 x(x-1,5)(x+6)}=0
$$
ma w zbiorze liczb rzeczywistych
A. dokładnie jedno rozwiązanie: $$x=2$$.
B. dokładnie dwa rozwiązania: $$x=1,5, x=2$$.
C. dokładnie trzy rozwiązania: $$x=-6, x=0, x=2$$.
D. dokładnie cztery rozwiązania: $$x=-6, x=0, x=1,5, x=2$$.
A
Zadanie 5. [2022 marzec, zad.8, 1 pkt]
Spośród rysunków A-D wybierz ten, na którym prawidłowo zaznaczono na osi liczbowej zbiór wszystkich liczb rzeczywistych spełniających nierówność:
$$
|x+1| \leq 2
$$
A
Zadanie 6. [2022 wrzesień, zad.6, 3 pkt]
Rozwiąż równanie
$$
3 x^3-6 x^2-27 x+54=0
$$
Przekształcamy lewą stronę równania do postaci iloczynu:
$$
\begin{gathered}
3 x^3-6 x^2-27 x+54=0 \\
3 x^2(x-2)-27(x-2)=0 \\
(x-2)\left(3 x^2-27\right)=0 \\
3(x-2)\left(x^2-9\right)=0
\end{gathered}
$$
Stąd otrzymujemy kolejno
$$
\begin{gathered}
x-2=0 \text { lub } \quad x^2-9=0 \\
x-2=0 \text { lub }(x-3)(x+3)=0 \\
x-2=0 \text { lub } x-3=0 \text { lub } x+3=0 \\
x=2 \text { lub } x=3 \text { lub } x=-3
\end{gathered}
$$
Zadanie 7. [2022 wrzesień, zad.7, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Równanie
$$
\frac{\left(x^2+x\right)(x+3)(x-1)}{x^2-1}=0
$$
ma w zbiorze liczb rzeczywistych dokładnie
A. jedno rozwiązanie: $$x=-3$$.
B. dwa rozwiązania: $$x=-3, x=0$$.
C. trzy rozwiązania: $$x=-3, x=-1, x=0$$.
D. cztery rozwiązania: $$x=-3, x=-1, x=0, x=1$$.
B
Komentarz
Wyznaczamy dziedzinę rówhania: $$D=R \backslash\{-1,1\}$$.
Licznik ułamka jest równy 0 , gdy
$$
\left(x^2+x\right)=0 \text { lub }(x+3)=0 \text { lub }(x-1)=0
$$
Zaten
$$
\begin{gathered}
x(x+1)=0 \text { lub } x=-3 \text { lub } x=1 \\
x=0 \text { lub } x=-1 \text { lub } x=-3 \text { lub } x=1
\end{gathered}
$$
Spośród tych czterech liczb do dziedziny należą tylko $$x=-3$$ oraz $$x=0$$,
Zadanie 8. [2022 wrzesień, zad.8, 1 pkt]
Spośród nierówności A-D wybierz tę, której zbiór wszystkich rozwiązań zaznaczono na osi liczbowej.
A. $$|x+2| \leq 2$$
B. $$|x-2| \leq 2$$
C. $$|x+2| \geq 2$$
D. $$|x-2| \geq 2$$
C
Komentarz
Dany zbiór składa się z dwóch przedzialów, których końce są równo odległe od liczby (-2). Z własności wartości bezwzględnej mamy, że
$$|x-a| \geq r$$ wtedy i tylko wtedy, gdy $$x \leq a-r$$ lub $$x \geq a+r$$.
Zatem uwzględniając interpretację geometryczną możemy stwierdzić, że rozwiązaniem jest $$\mathrm{C}$$
Zadanie 9. [2022 Zbiór zadań CKE, zad.14, 2 pkt]
Rozwiąż nierówność. Podaj największą liczbę całkowitą spełniającą tę nierówność.
$$
2 x \geq \sqrt{5} \cdot x+3 \sqrt{5}-6
$$
Nierówność $$2 x \geq \sqrt{5} \cdot x+3 \sqrt{5}-6$$ przekształcamy równoważnie:
$$
\begin{aligned}
&2 x \geq \sqrt{5} \cdot x+3 \sqrt{5}-6 \\
&2 x-\sqrt{5} \cdot x \geq 3 \sqrt{5}-6 \\
&(2-\sqrt{5}) \cdot x \geq 3 \sqrt{5}-6
\end{aligned}
$$
Dzielimy obie strony nierówności przez $$(2-\sqrt{5})$$. Ponieważ liczba ta jest ujemna, więc należy pamiętać o odpowiedniej zmianie zwrotu nierówności.
$$
x \leq \frac{3 \sqrt{5}-6}{2-\sqrt{5}}
$$
Upraszczamy ułamek $$\frac{3 \sqrt{5}-6}{2-\sqrt{5}}$$
$$
\begin{gathered}
x \leq \frac{-3(2-\sqrt{5})}{2-\sqrt{5}} \\
x \leq-3
\end{gathered}
$$
Zbiorem wszystkich rozwiązań nierówności $$2 x \geq \sqrt{5} \cdot x+3 \sqrt{5}-6$$ jest $$(-\infty,-3]$$. Największą liczbą całkowitą, która spełnia tę nierówność jest ( $$-3)$$.
Uwaga
Ułamek $$\frac{3 \sqrt{5}-6}{2-\sqrt{5}}$$ możemy uprościć, usuwając niewymierność z mianownika:
$$
\frac{3 \sqrt{5}-6}{2-\sqrt{5}}=\frac{3 \sqrt{5}-6}{2-\sqrt{5}} \cdot \frac{2+\sqrt{5}}{2+\sqrt{5}}=\frac{6 \sqrt{5}+15-12-6 \sqrt{5}}{2^2-(\sqrt{5})^2}=\frac{3}{-1}=-3
$$
Zadanie 10. [2022 Zbiór zadań CKE, zad.15, 2 pkt]
Rozwiąż równanie
$$
-2 x^3+x^2+18 x-9=0
$$
Sposób I
Zapisujemy lewą stronę równania w postaci iloczynowej, stosując metodę grupowania wyrazów
$$
-x^2(2 x-1)-9(2 x-1)=0 \text { lub } 2 x\left(-x^2+9\right)-1\left(-x^2+9\right)=0
$$
Stąd
$$
\begin{gathered}
\left(-x^2+9\right)(2 x-1)=0 \\
(3-x)(3+x)(2 x-1)=0
\end{gathered}
$$
Zatem rozwiązaniami równania są: $$x=-3$$ lub $$x=\frac{1}{2}$$ lub $$x=3$$.
Sposób II
Korzystamy z definicji podzielności wielomianu $$\mathrm{W}(x)$$ przez dwumian $$(x-a)$$. Obliczamy $$W(3)=0$$ i stwierdzamy, że liczba 3 jest pierwiastkiem wielomianu
$$W(x)=-2 x^3+x^2+18 x-9$$. Po podzieleniu wielomianu $$W$$ przez dwumian $$(x-3)$$ otrzymujemy iloraz $$\left(-2 x^2-5 x+3\right)$$.
Zapisujemy dane równanie w postaci
$$
(x-3)\left(-2 x^2-5 x+3\right)=0
$$
Stąd
$$
x-3=0, \text { lub }-2 x^2-5 x+3=0
$$
Rozwiązując równanie kwadratowe, otrzymamy:
$$
\begin{gathered}
\Delta=(-5)^2-4 \cdot(-2) \cdot 3=25+24=49 \\
x_1=\frac{5-\sqrt{49}}{2 \cdot(-2)}=\frac{5-7}{-4}=\frac{-2}{-4}=\frac{1}{2} \text { oraz } x_2=\frac{5+\sqrt{49}}{2 \cdot(-2)}=\frac{5+7}{-4}=\frac{12}{-4}=-3
\end{gathered}
$$
Rozwiązując równanie $$x-3=0$$, otrzymujemy: $$x=3$$.
Rozwiązania równania to: $$x=\frac{1}{2}$$ lub $$x=-3$$ lub $$x=3$$.
Zadanie 11. [2022 Zbiór zadań CKE, zad.16, 3 pkt]
Rozwiąż równanie
$$
-x^3+13 x-12=0
$$
Sposób I
Przekształcamy lewą stronę równania $$-x^3+13 x-12=0$$ w sposób równoważny tak, aby otrzymać postać iloczynową wielomianu $$-x^3+13 x-12$$ :
$$
\begin{gathered}
-x^3+13 x-12=0 \\
-x^3+x+12 x-12=0 \\
-x\left(x^2-1\right)+12(x-1)=0 \\
-x(x-1)(x+1)+12(x-1)=0 \\
(x-1)[-x(x+1)+12]=0 \\
(x-1)\left(-x^2-x+12\right)=0
\end{gathered}
$$
Korzystamy z własności iloczynu i zapisujemy równanie $$(x-1)\left(-x^2-x+12\right)=0$$ jako alternatywę równań:
$$
x-1=0 \quad \text { lub } \quad-x^2-x+12=0
$$
Rozwiązując równanie $$x-1=0$$, otrzymujemy: $$x=1$$
Rozwiązując równanie kwadratowe, otrzymamy:
$$
\begin{gathered}
\Delta=(-1)^2-4 \cdot(-1) \cdot 12=49 \\
x=\frac{1+7}{-2}=-4 \text { lub } x=\frac{1-7}{-2}=3
\end{gathered}
$$
Zatem rozwiązaniami równania są liczby: $$(-4), 1$$ oraz 3.
Sposób II
Korzystamy z definicji podzielności wielomianu $$\mathrm{W}(x)$$ przez dwumian $$(x-a)$$.
Obliczamy $$W(1)=0$$ i stwierdzamy, że liczba 1 jest pierwiastkiem wielomianu
$$
W(x)=-x^3+13 x-12=0
$$
Po podzieleniu wielomianu $$W$$ przez dwumian $$(x-1)$$ otrzymujemy iloraz $$\left(-x^2-x+12\right)$$.
Zapisujemy dane równanie w postaci
$$
(x-1)\left(-x^2-x+12\right)=0
$$
Stąd
$$
x-1=0 \text { lub }-x^2-x+12=0
$$
Rozwiązując równanie kwadratowe, otrzymamy:
$$
\begin{aligned}
&\Delta=(-1)^2-4 \cdot(-1) \cdot 12=49 \\
&x=\frac{1+7}{-2}=-4 \text { lub } x=\frac{1-7}{-2}=3
\end{aligned}
$$
Rozwiązując równanie $$x-1=0$$, otrzymujemy: $$x=1$$
Rozwiązania równania to: $$x=-4$$ lub $$x=1$$ lub $$x=3$$.
Zadanie 12. [2022 Zbiór zadań CKE, zad.18, 1 pkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Równanie
$$
\frac{\left(3 x^2-6 x\right)\left(x^2-9\right)}{(x-2)(x-3)^2}=0
$$
w zbiorze liczb rzeczywistych
A. nie ma rozwiązań.
B. ma dokładnie jedno rozwiązanie: $$x=0$$.
C. ma dokładnie dwa rozwiązania: $$x=0, x=-3$$.
D. ma dokładnie cztery rozwiązania: $$x=0, x=2, x=3, x=-3$$.
C
Komentarz
Stosując wzory skróconego mnożenia na: $$(a+b)^2,(a-b)^2, a^2-b^2[\ldots]$$, otrzymujemy:
$$
\frac{3 x(x-2)(x-3)(x+3)}{(x-2)(x-3)^2}=0
$$
Stąd
$$3 x=0$$ lub $$x-2=0$$ lub $$x-3=0$$ lub $$x+3=0$$
Zatem $$x=0$$ lub $$x=2$$ lub $$x=3$$ lub $$x=-3$$.
Ponieważ równanie ma sens, gdy $$x \neq 2$$ lub $$x \neq 3$$, więc jego rozwiązaniami są liczby
$$
x=0, x=-3 \text {. }
$$
Zadanie 13. [2022 grudzień, zad.8, (1 pkt)]
Dana jest nierówność kwadratowa
$$(3 x-9)(x+k)<0$$
z niewiadomą $$x$$ i parametrem $$k \in \mathbb{R}$$. Rozwiązaniem tej nierówności jest przedział ( $$-2,3)$$.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba $$k$$ jest równa
A. (-2)
B. 2
C. (-3)
D. 3
B
Zadanie 14. [2022 grudzień, zad.12, (1 pkt)]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Równanie $$\frac{(4-x)(2 x-3)}{(3 x-5)(3-2 x)}=0$$ w zbiorze liczb rzeczywistych ma dokładnie
A. jedno rozwiązanie.
B. dwa rozwiązania.
C. trzy rozwiązania.
D. cztery rozwiązania.
A
Zadanie 15. [2022 grudzień, zad.13, (1 pkt)]
Dana jest nierówność
$$
2-\frac{x}{2} \geq \frac{x}{3}-3
$$
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Największą liczbą całkowitą, która spelnia tę nierówność, jest
A. 6
B. 5
C. 7
D. (-6)
A
Zadanie 16. [2023 maj, zad.1, (1 pkt)]
Na osi liczbowej zaznaczono sumę przedziałów.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Zbiór zaznaczony na osi jest zbiorem wszystkich rozwiązań nierówności
A. $$|x-3,5| \geq 1,5$$
B. $$|x-1,5| \geq 3,5$$
C. $$|x-3,5| \leq 1,5$$
D. $$|x-1,5| \leq 3,5$$
B
Zadanie 17. [2023 maj, zad.6, (1 pkt)]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Zbiorem wszystkich rozwiązań nierówności
$$
-2(x+3) \leq \frac{2-x}{3}
$$
jest przedział
A. $$(-\infty,-4]$$
B. $$(-\infty, 4]$$
C. $$[-4, \infty)$$
D. $$[4, \infty)$$
C
Zadanie 18. [2023 maj, zad.7, (1 pkt)]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Jednym z rozwiązań równania $$\sqrt{3}\left(x^2-2\right)(x+3)=0$$ jest liczba
A. 3
B. 2
C. $$\sqrt{3}$$
D. $$\sqrt{2}$$
D
Zadanie 19. [2023 maj, zad.8, (1 pkt)]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Równanie $$\frac{(x+1)(x-1)^2}{(x-1)(x+1)^2}=0$$ w zbiorze liczb rzeczywistych
A. nie ma rozwiązania.
B. ma dokładnie jedno rozwiązanie: -1 .
C. ma dokładnie jedno rozwiązanie: 1 .
D. ma dokładnie dwa rozwiązania: -1 oraz 1 .
A
Zadanie 20. [2023 maj, zad.9, (3 pkt)]
Rozwiąż równanie
$$
3 x^3-2 x^2-12 x+8=0
$$
Zapisz obliczenia.
Sposób I
Przekształcamy równanie równoważnie i stosujemy metodę grupowania wyrazów:
$$
\begin{gathered}
3 x^3-2 x^2-12 x+8=0 \\
x^2(3 x-2)-4(3 x-2)=0 \\
(3 x-2)\left(x^2-4\right)=0 \\
(3 x-2)(x-2)(x+2)=0 \\
3 x-2=0 \text { lub } x-2=0 \text { lub } x+2=0 \\
x=\frac{2}{3} \text { lub } x=2 \text { lub } x=-2
\end{gathered}
$$
Rozwiązaniami równania są liczby: $$(-2), \frac{2}{3}, 2$$.
Sposób II
Przekształcamy równanie równoważnie i stosujemy metodę grupowania wyrazów:
$$
3 x^3-2 x^2-12 x+8=0
$$
$$
\begin{gathered}
3 x\left(x^2-4\right)-2\left(x^2-4\right)=0 \\
(3 x-2)\left(x^2-4\right)=0 \\
(3 x-2)(x-2)(x+2)=0 \\
3 x-2=0 \text { lub } x-2=0 \text { lub } x+2=0 \\
x=\frac{2}{3} \text { lub } x=2 \text { lub } x=-2
\end{gathered}
$$
Rozwiązaniami równania są liczby: $$(-2), \frac{2}{3}, 2$$.
Sposób III
Obliczamy $$W(2)=0$$ i stwierdzamy, że liczba 2 jest pierwiastkiem wielomianu $$W(x)=3 x^3-2 x^2-12 x+8$$.
Zatem wielomian $$W$$ jest podzielny przez dwumian $$x-2$$. Dzielimy wielomian $$W$$ przez dwumian $$x-2$$ i otrzymujemy
$$
\left(3 x^3-2 x^2-12 x+8\right):(x-2)=3 x^2+4 x-4
$$
Zatem $$W(x)=(x-2)\left(3 x^2+4 x-4\right)$$.
Obliczamy pierwiastki trójmianu $$3 x^2+4 x-4$$ :
$$
\begin{gathered}
\Delta=4^2-4 \cdot 3 \cdot(-4)=64 \\
x=\frac{-4-8}{2 \cdot 3}=-2 \text { oraz } x=\frac{-4+8}{2 \cdot 3}=\frac{2}{3}
\end{gathered}
$$
Rozwiązaniami równania są liczby: $$(-2), \frac{2}{3}, 2$$.
Sposób IV
Obliczamy $$W(2)=0$$ i stwierdzamy, że liczba 2 jest pierwiastkiem wielomianu $$W(x)=3 x^3-2 x^2-12 x+8$$
Obliczamy $$W(-2)=0$$ i stwierdzamy, że liczba $$(-2)$$ jest pierwiastkiem wielomianu $$W(x)=3 x^3-2 x^2-12 x+8$$.
Obliczamy $$W\left(\frac{2}{3}\right)=0$$ i stwierdzamy, że liczba $$\frac{2}{3}$$ jest pierwiastkiem wielomianu $$W(x)=3 x^3-2 x^2-12 x+8$$.
Ponieważ $$W$$ jest wielomianem stopnia trzeciego, więc ma co najwyżej trzy pierwiastki rzeczywiste. Oznacza to, że jedynymi rozwiązaniami równania $$3 x^3-2 x^2-12 x+8=0$$ są liczby: $$(-2), \frac{2}{3}, 2$$.
Zadanie 21. [2023 czerwiec, zad.1, (1 pkt)]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wszystkich liczb całkowitych dodatnich spełniających nierówność $$|x+5|<15$$ jest
A. 9
B. 10
C. 20
D. 21
A
Zadanie 22. [2023 czerwiec, zad.8, (2 pkt)]
Rozwiąż nierówność
$$
x(2 x-1)<2 x
$$
Zapisz obliczenia.
Przekształcamy nierówność równoważnie:
$$
\begin{gathered}
x(2 x-1)<2 x \\
2 x^2-x-2 x<0 \\
2 x^2-3 x<0 \\
2 x\left(x-\frac{3}{2}\right)<0
\end{gathered}
$$
Odczytujemy i zapisujemy pierwiastki trójmianu $$2 x\left(x-\frac{3}{2}\right): x=0$$ lub $$x=\frac{3}{2}$$. Podajemy zbiór rozwiązań nierówności: $$\left(0, \frac{3}{2}\right)$$ lub $$x \in\left(0, \frac{3}{2}\right)$$, lub zaznaczamy zbiór rozwiązań na osi liczbowej
Inny sposób realizacji obliczenia pierwiastków trójmianu:
Przekształcamy równoważnie nierówność do postaci $$2 x^2-3 x<0$$, obliczamy wyróżnik $$\Delta$$ trójmianu $$2 x^2-3 x$$, a następnie pierwiastki tego trójmianu:
$$
\begin{gathered}
\Delta=(-3)^2-4 \cdot 2 \cdot 0=9 \\
x=\frac{-(-3)-3}{2 \cdot 2}=0 \text { lub } x=\frac{-(-3)+3}{2 \cdot 2}=\frac{3}{2}
\end{gathered}
$$
Zadanie 23. [2023 czerwiec, zad.9, (3 pkt)]
Rozwiąż równanie
$$
x^3+4 x^2-9 x-36=0
$$
Zapisz obliczenia.
Przekształcamy równanie równoważnie i stosujemy metodę grupowania wyrazów:
$$
\begin{gathered}
x^3+4 x^2-9 x-36=0 \\
x^2(x+4)-9(x+4)=0 \\
(x+4)\left(x^2-9\right)=0 \\
(x+4)(x+3)(x-3)=0 \\
x+4=0 \text { lub } x+3=0 \text { lub } x-3=0 \\
x=-4 \text { lub } x=-3 \text { lub } x=3
\end{gathered}
$$
Rozwiązaniami równania są liczby: $$(-4),(-3), 3$$.
Zadanie 24. [2023 czerwiec, zad.10, (1 pkt)]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Równanie $$\frac{\left(x^2-3 x\right)(x+2)}{x^2-4}=0$$ w zbiorze liczb rzeczywistych ma dokładnie
A. jedno rozwiązanie.
B. dwa rozwiązania.
C. trzy rozwiązania.
D. cztery rozwiązania.
B
Zadanie 25. [2023 sierpień, zad.1, (1 pkt)]
Dana jest nierówność
\[|x-5|<2\]
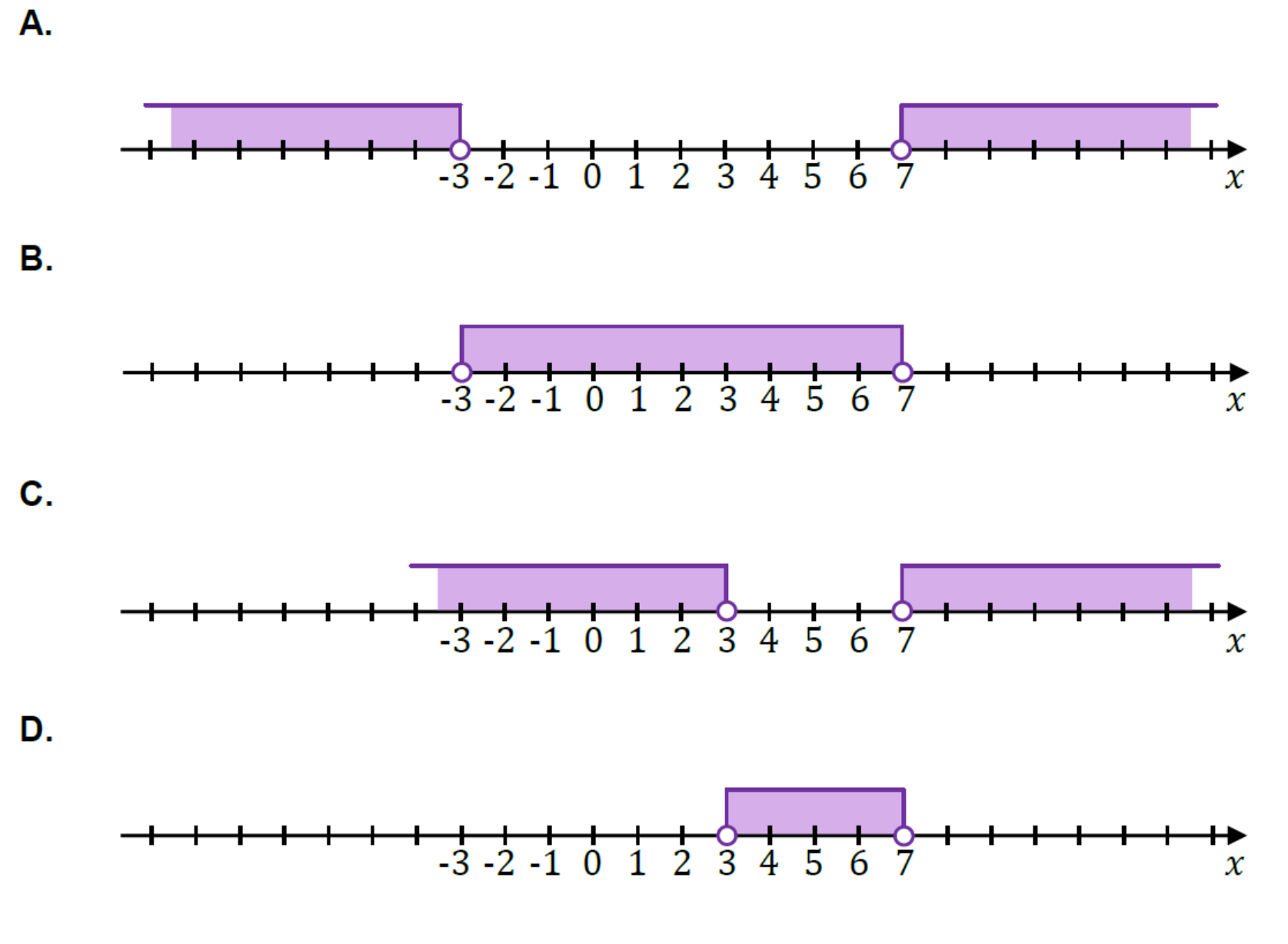
Na którym rysunku poprawnie zaznaczono na osi liczbowej zbiór wszystkich liczb rzeczywistych spełniających powyższą nierówność? Wybierz właściwą odpowiedź spośród podanych.
D
Zadanie 26. [2023 sierpień, zad.8, (1 pkt)]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Równanie \(\frac{\left(x^{2}-3 x\right)\left(x^{2}+1\right)}{x^{2}-25}=0\) w zbiorze liczb rzeczywistych ma dokładnie
A. jedno rozwiązanie.
B. dwa rozwiązania.
C. trzy rozwiązania.
D. cztery rozwiązania.
B
Zadanie 27. [2023 sierpień, zad.9, (3 pkt)]
Rozwiąż równanie
\[3 x^{3}-2 x^{2}-3 x+2=0\]
Zapisz obliczenia.
Przekształcamy równanie równoważnie i stosujemy metodę grupowania wyrazów:
\[\begin{gathered}
3 x^{3}-2 x^{2}-3 x+2=0 \\
x^{2}(3 x-2)-(3 x-2)=0 \\
(3 x-2)\left(x^{2}-1\right)=0 \\
(3 x-2)(x-1)(x+1)=0 \\
3 x-2=0 \quad \text { lub } x-1=0 \quad \text { lub } x+1=0 \\
x=\frac{2}{3} \quad \text { lub } x=1 \text { lub } x=-1
\end{gathered}\]
Rozwiązaniami równania są liczby: \((-1), \frac{2}{3}, 1\).
Zadanie 28. [2023 grudzień, zad.4, (1 pkt)]
Na osi liczbowej zaznaczono przedział.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Zbiór zaznaczony na osi jest zbiorem wszystkich rozwiązań nierówności
A. \(|x-2|<5\)
B. \(|x-2|>5\)
C. \(|x-5|<2\)
D. \(|x-5|>2\)
A
Zadanie 29. [2023 grudzień, zad.9, (3 pkt)]
Rozwiąż równanie
\[2 x^{3}+3 x^{2}=10 x+15\]
Zapisz obliczenia.
Przekształcamy równanie równoważnie, stosując metodę grupowania wyrazów:
\[\begin{gathered}
2 x^{3}+3 x^{2}=10 x+15 \\
2 x^{3}+3 x^{2}-10 x-15=0 \\
x^{2}(2 x+3)-5(2 x+3)=0 \\
(2 x+3)\left(x^{2}-5\right)=0
\end{gathered}\]
\[\begin{gathered}
(2 x+3)(x-\sqrt{5})(x+\sqrt{5})=0 \\
2 x+3=0 \quad \text { lub } \quad x-\sqrt{5}=0 \quad \text { lub } \quad x+\sqrt{5}=0 \\
x=-\frac{3}{2} \quad \text { lub } \quad x=\sqrt{5} \quad \text { lub } \quad x=-\sqrt{5}
\end{gathered}\]
Rozwiązaniami równania są liczby: \((-\sqrt{5}),\left(-\frac{3}{2}\right), \sqrt{5}\).
Zadanie 30. [2024 maj, zad.1, (1 pkt)]
Dana jest nierówność
\[|x-1| \geq 3\]
Na którym rysunku poprawnie zaznaczono na osi liczbowej zbiór wszystkich liczb rzeczywistych spełniających powyższą nierówność? Wybierz właściwą odpowiedź spośród podanych.
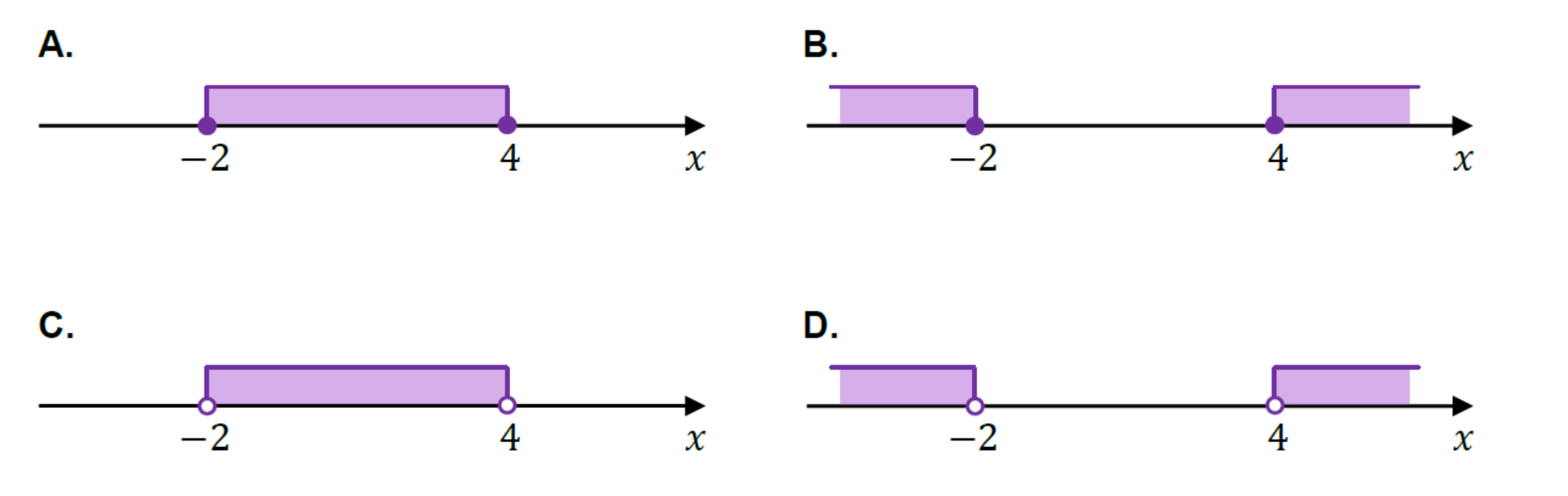
B
Zadanie 31. [2024 czerwiec, zad.6, (1 pkt)]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba wszystkich całkowitych dodatnich rozwiązań nierówności
\[\frac{3 x-5}{12}<\frac{1}{3}\]
jest równa
A. 2
B. 3
C. 5
D. 6
A
Zadanie 32. [2024 czerwiec, zad.10, (3 pkt)]
Rozwiąż równanie
\[4 x^{3}-12 x^{2}-x+3=0\]
Zapisz obliczenia.
Przeksztalcamy równanie równoważnie i stosujemy metodę grupowania wyrazów:
\[\begin{gathered}
4 x^3-12 x^2-x+3=0 \\
4 x^2(x-3)-(x-3)=0 \\
(x-3)\left(4 x^2-1\right)=0 \\
(x-3)(2 x-1)(2 x+1)=0 \\
x-3=0 \text { lub } 2 x-1=0 \text { lub } 2 x+1=0 \\
x=3 \text { lub } x=\frac{1}{2} \text { lub } x=-\frac{1}{2}
\end{gathered}\]
Rozwiązaniami równania są liczby: \(\left(-\frac{1}{2}\right), \frac{1}{2}, 3\).
Zadanie 33. [2024 grudzień, zad.8, (3 pkt)]
Rozwiąż równanie
\[
\frac{x+3}{x-1}=\frac{x}{2 x-2}
\]
Zapisz konieczne założenie i obliczenia.
Sposób I
Każde z wyrażeń: \(\frac{x+3}{x-1}, \frac{x}{2 x-2}\) ma sens liczbowy dla \(x \neq 1\).
Przekształcamy równanie równoważnie:
\[
\begin{gathered}
\frac{x+3}{x-1}=\frac{x}{2 x-2} / \cdot 2(x-1), \text { gdzie } x \neq 1 \\
2(x+3)=x, \text { gdzie } x \neq 1
\end{gathered}
\]
Rozwiązujemy otrzymane równanie liniowe:
\[
\begin{gathered}
2 x+6=x \\
x=-6
\end{gathered}
\]
Rozwiązaniem równania \(\frac{x+3}{x-1}=\frac{x}{2 x-2}\) jest liczba (-6).
Sposób II
Każde z wyrażeń: \(\frac{x+3}{x-1}, \frac{x}{2 x-2}\) ma sens liczbowy dla \(x \neq 1\).
Przekształcamy równanie równoważnie:
\[
\begin{gathered}
\frac{x+3}{x-1}=\frac{x}{2 x-2} \\
(x+3)(2 x-2)=x(x-1), \text { gdzie } x \neq 1
\end{gathered}
\]
Rozwiązujemy otrzymane równanie kwadratowe:
\[
\begin{gathered}
2 x^{2}-2 x+6 x-6=x^{2}-x \\
x^{2}+5 x-6=0
\end{gathered}
\]
Obliczamy wyróżnik trójmianu \(x^{2}+5 x-6\) :
\[
\Delta=5^{2}-4 \cdot 1 \cdot(-6)=49
\]
Stąd
\[
\begin{aligned}
& x_{1}=\frac{-5-\sqrt{49}}{2 \cdot 1}=-6 \\
& x_{2}=\frac{-5+\sqrt{49}}{2 \cdot 1}=1
\end{aligned}
\]
Wobec założenia \(x \neq 1\) jedynym rozwiązaniem równania \(\frac{x+3}{x-1}=\frac{x}{2 x-2}\) jest liczba ( -6 ).
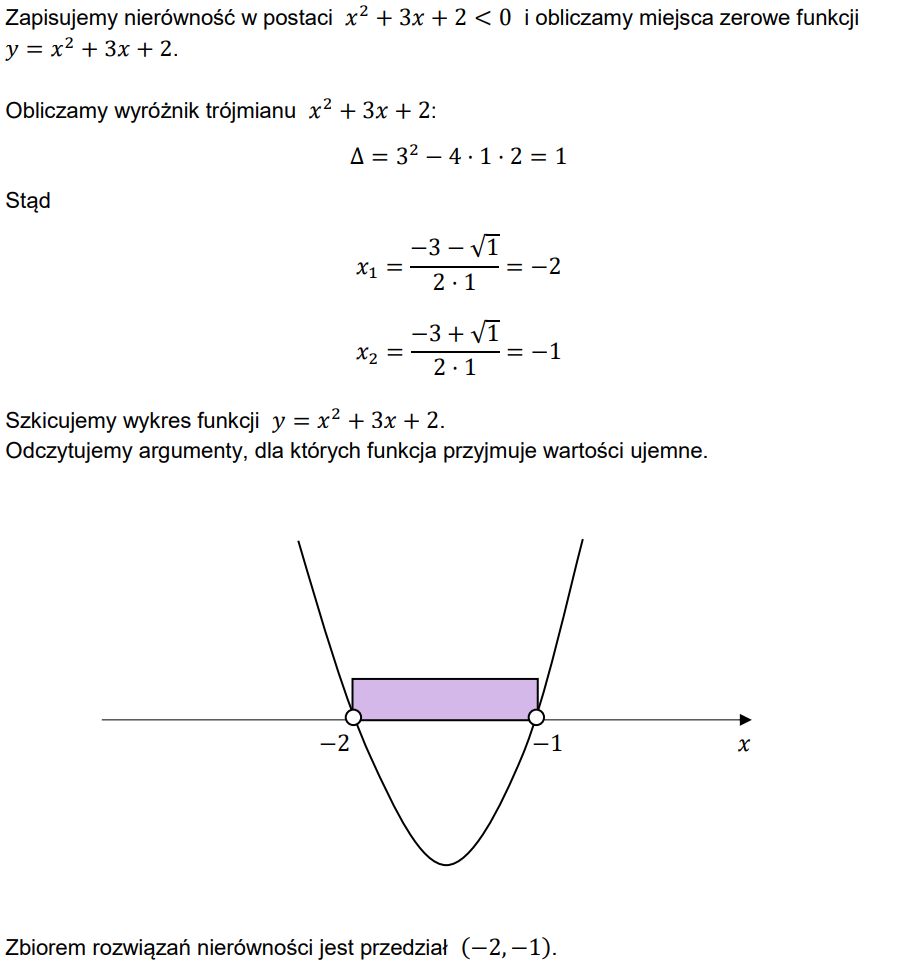
Zadanie 34. [2024 grudzień, zad.9, (2 pkt)]
Rozwiąż nierówność
\[
x(x-6) \leq 7
\]
Zapisz obliczenia.
Zapisujemy nierówność w postaci \(x^{2}-6 x-7 \leq 0\) i obliczamy miejsca zerowe funkcji \(y=x^{2}-6 x-7\).
Obliczamy wyróżnik trójmianu \(x^{2}-6 x-7\) :
\[
\Delta=(-6)^{2}-4 \cdot 1 \cdot(-7)=64
\]
Stąd
\[
\begin{aligned}
& x_{1}=\frac{-(-6)-\sqrt{64}}{2 \cdot 1}=-1 \\
& x_{2}=\frac{-(-6)+\sqrt{64}}{2 \cdot 1}=7
\end{aligned}
\]
Szkicujemy wykres funkcji \(y=x^{2}-6 x-7\).
Odczytujemy argumenty, dla których funkcja przyjmuje wartości niedodatnie.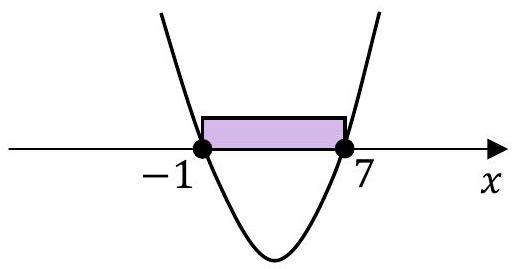
Zbiorem rozwiązań nierówności jest przedział [-1, 7].
Zadanie 35. [2024 sierpień, zad.1, (1 pkt)]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba wszystkich całkowitych rozwiązań nierówności \(|x+1|<3\) jest równa
A. 2
B. 3
C. 5
D. 7
C
Zadanie 36. [2024 sierpień, zad.5, (1 pkt)]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Zbiorem wszystkich rozwiązań nierówności
\[
\frac{3(6-x)}{17} \leq 3
\]
jest przedział
A. \((-\infty,-11)\)
B. \((-\infty,-11]\)
C. \((-11,+\infty)\)
D. \([-11,+\infty)\)
D
Zadanie 37. [2024 sierpień, zad.6, (1 pkt)]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Równanie \(\frac{x(x+5)(2-x)}{2 x+4}=0\) w zbiorze liczb rzeczywistych ma dokładnie
A. dwa rozwiązania: \((-5)\) oraz 2 .
B. dwa rozwiązania: (-5) oraz 0 .
C. trzy rozwiązania: \((-5), 0\) oraz 2 .
D. cztery rozwiązania: \((-5),(-2), 0\) oraz 2 .
C
Zadanie 38. [2024 sierpień, zad.7, (3 pkt)]
Rozwiąż równanie
\[
x^3+5 x^2-2 x-10=0
\]
Zapisz obliczenia.
Przekształcamy równanie równoważnie i stosujemy metodę grupowania wyrazów:
\[
\begin{gathered}
x^3+5 x^2-2 x-10=0 \\
x\left(x^2-2\right)+5\left(x^2-2\right)=0 \\
(x+5)\left(x^2-2\right)=0 \\
(x+5)(x-\sqrt{2})(x+\sqrt{2})=0 \\
x+5=0 \quad \text { lub } \quad x-\sqrt{2}=0 \quad \text { lub } \quad x+\sqrt{2}=0 \\
x=-5 \quad \text { lub } \quad x=\sqrt{2} \quad \text { lub } \quad x=-\sqrt{2}
\end{gathered}
\]
Rozwiązaniami równania są liczby: \((-5),(-\sqrt{2}), \sqrt{2}\).
Zadanie 39. [2025 maj, zad.6, (1 pkt)]

D
Zadanie 40. [2025 maj, zad.7, (1 pkt)]

A
Zadanie 41. [2025 maj, zad.10, (2 pkt)]
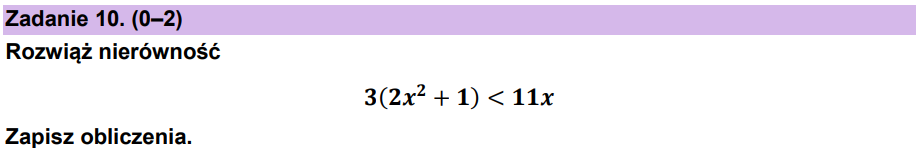

Zadanie 42. [2025 czerwiec, zad.1, (1 pkt)]

B
Zadanie 43. [2025 czerwiec, zad.6, (1 pkt)]

C
Zadanie 44. [2025 czerwiec, zad.7, (1 pkt)]

B
Zadanie 45. [2025 czerwiec, zad.9, (2 pkt)]
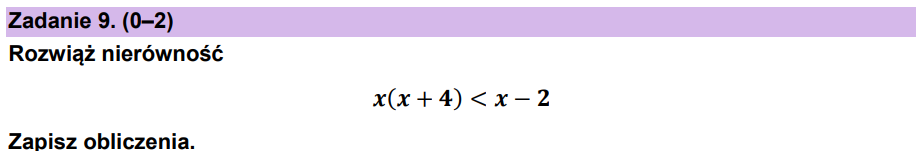
Zadanie 46. [2025 sierpień, zad.7, (1 pkt)]

A
Zadanie 47. [2025 sierpień, zad.8, (3 pkt)]


Zadanie 48. [2025 sierpień, zad.9, (2 pkt)]
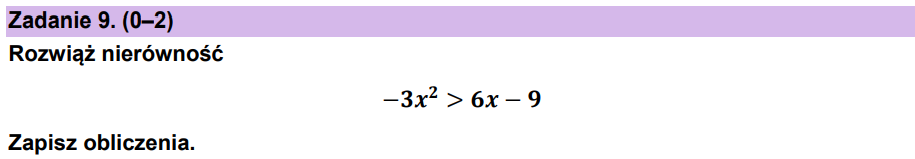
![]()
Zadanie 49. [2025 sierpień, zad.10, (1 pkt)]

C