1975 woj. białostockie - profil podstawowy
Zadanie 1.
Dla jakich wartości parametru $$m$$, pierwiastki równania
$$
\frac{m x}{m-1}+\frac{m+1}{x}=x+1
$$
speiniają nierówność $$\frac{1}{x_1}+\frac{1}{x_2}<2 m+1$$ ?
Zadanie 2.
Punkty $$A(7,7), B(0,8), C(-2,4)$$ są wierzchołkami trójkąta $$A B C$$.
a) Oblicz pole i miary kątów trójkąta $$A B C$$.
b) Napisz równanie okręgu opisanego na trójkącie $$A B C$$.
c) Napisz równanie stycznej w punkcie $$M(3,9)$$ do okręgu opisanego na trójkącie $$A B C$$.
Zadanie 3.
W trapezie $$A B C D$$ dane są $$A C=a, kąt D A C=kąt A B C=\alpha$$. Proste $$A D$$ i $$B C$$, w których zawierają się ramiona trapezu, są prostopadłe. Oblicz pole trapezu.
Zadanie 4.
Obwód trójkąta równoramiennego jest równy $$18 \mathrm{~cm}$$. Jakie powinny być boki tego trójkąta, by objętość bryly powstałej z jego obrotu dokoła podstawy była największa?
Zadanie 5.
Dwudziestoosobowa grupa studencka, w której jest $$6$$ kobiet, otrzymała $$5$$ biletów do teatru. Bilety rozdzieliło się drogą losowania. Jakie jest prawdopodobieństwo, że wśród posiadaczy biletów znajdą się dokładnie $$3$$ kobiety.
Zadanie 1.
$$-\frac{3}{2}<m<-1 \vee 0<m<1$$.
Zadanie 2.
a) $$P_{\triangle \mathrm{ABC}}=15$$.
$$\cos (\overrightarrow{A B}, \overrightarrow{A C})=\frac{2}{\sqrt{5}}$$,
$$\cos (\overrightarrow{C A}, \overrightarrow{C B})=\frac{1}{\sqrt{2}} \Rightarrow |kąt(\overrightarrow{C A}, \overrightarrow{C B})|=\frac{\pi}{4}$$,
$$\cos \overrightarrow{(B C}, \overrightarrow{B A})=-\frac{1}{\sqrt{10}}$$.
b) $$Q:(x-3)^2+(y-4)^2=25$$
c) Równanie stycznej do okręgu $$Q$$ w punkcie $$M$$ ma postać $$y=9$$.
Zadanie 3.
$$P=a^2 \operatorname{ctg} 2 \alpha$$.
Zadanie 4.
Podstawa trójkąta równa $$\frac{9}{2} \mathrm{~cm}$$, a ramiona po $$\frac{27}{4} \mathrm{~cm}$$.
Zadanie 5.
$$p=\frac{\left(\begin{array}{c}14 \\ 2\end{array}\right)\left(\begin{array}{l}6 \\ 3\end{array}\right)}{\left(\begin{array}{c}20 \\ 5\end{array}\right)}$$
1975 woj. białostockie - profil matematyczno - fizyczny
Zadanie 1. Dla jakich wartości parametru $$a$$ równanie
$$
3 x^2-x \log a+1=0
$$
ma pierwiastki rzeczywiste spełniające warunek $$x_1^2+x_2^2=1$$ ?
Zadanie 2. Znajdź równania stycznych do okręgu
$$
x^2+y^2-8 x-10 y+28=0
$$
i nachylonych do prostej $$5 x-y+3=0$$ pod kątem $$\frac{\pi}{4}$$.
Zadanie 3. W półokrąg o promieniu $$R$$ wpisano trapez, którego podstawą jest średnica okręgu. Dla jakiego kąta przy podstawie trapezu pole trapezu jest największe?
Zadanie 4. Przekątne $$\overline{A C}$$ i $$\overline{B D}$$ trapezu $$A B C D$$ o podstawach $$\overline{A B}$$ i $$\overline{D C}$$ przecinają się w punkcie $$O$$. Mając dane pola $$P_1$$ i $$P_2$$ trójkątów $$A B O$$ i $$C D O$$ oblicz pole trapezu.
Zadanie 5. Dziesięciu chłopców wybrało się na wycieczkę rowerową jadąc gęsiego. Janek i Franek oraz Bronek znajdują się w grupie chłopców. Jakie jest prawdopodobieństwo, że
a) Janka, Franka i Bronka nikt nie przedziela,
b) Janek i Franek znajdują się obok siebie, a Bronka od Janka i Franka przedziela co najmniej jeden chłopak.
Zadanie 1.
$$a_1=10^{-\sqrt{15}}$$ lub $$a_2=10^{\sqrt{15}}$$
Zadanie 2.
$$y=\frac{2}{3} x+\frac{20}{3}, y=\frac{2}{3} x-2, y=-\frac{3}{2} x+\frac{35}{2}, y=-\frac{3}{2} x+\frac{9}{2}$$
Zadanie 3.
Gdy $$\alpha=\frac{\pi}{3}$$ pole trapezu jest największe.
Zadanie 4.
$$P=\frac{1}{2}(a+b)\left(h_1+h_2\right)=P_1+P_2+a h_2=\left(\sqrt{P_1}+\sqrt{P_2}\right)^2$$
Zadanie 5.
a) $$ P(A)=\frac{3 ! 7 ! 8 !}{10 !}=\frac{1}{15} . $$
b) $$ P(B)=\frac{2 ! 8 ! 9 !-2 ! 7 ! 8 !}{10 !}=\frac{7}{45} .
$$
1975 woj. białostockie - profil humanistyczny
Zadanie 1. Dla jakich wartości parametru $$m$$ równanie
$$
x^2+(2 m-3) x+2 m+5=0
$$
ma dwa pierwiastki rzeczywiste różnych znaków?
Zadanie 2. Punkty $$A(6,-1), B(6,-5)$$ są wierzchołkami trójkąta równoramiennego $$A B C$$, w którym $$A B=A C$$. Wysokość $$\overline{A D}$$ trójkąta zawiera się w prostej o równaniu $$y=x-7$$.
a) Oblicz współrzędne wierzchołka $$C$$.
b) Oblicz pole trójkąta $$A B C$$.
c) Oblicz długość boku $$\overline{B C}$$.
Zadanie 3. Zbadaj przebieg funkcji $$f(x)=x^4-10 x^2+9$$ i sporządź jej wykres.
Zadanie 4. Osiem osób posadzono przy okrągłym stole. Przyjmując, że wszystkie sposoby, w jakie można to zrobić, są jednakowo prawdopodobne, oblicz prawdopodobieństwo zdarzenia, że ustalone dwie osoby będą siedziaty obok siebie.
Zadanie 5. Rozwiąż równanie $$3 \sin x=2 \cos ^2 x$$.
Zadanie 1.
$$m<-\frac{5}{2}$$
Zadanie 2.
a) $$C(2,-1)$$.
b) $$P_{\triangle A B C}=8$$.
c) $$|B C|=4 \sqrt{2}$$
Zadanie 3.
$$f^{\prime}(x)=4 x^3-20 x, \quad f^{\prime}(x)=0 \Rightarrow x=0 \vee x=-\sqrt{5} \vee x=\sqrt{5}$$
$$f^{\prime}(x)>0$$, dla $$x \in(-\sqrt{5} ; 0) \cup(\sqrt{5} ;+\infty)$$,
$$f^{\prime}(x)<0$$, dla $$x \in(-\infty ;-\sqrt{5}) \cup(0 ; \sqrt{5})$$,
Dla $$x=\pm \sqrt{5}$$ minima lokalne równe $$f(-\sqrt{5})=$$ $$-16=f(\sqrt{5})$$
Dla $$x=0$$ maksimum lokalne równe $$f(0)=9$$.
Miejsca zerowe: $$f(x)=0 \Rightarrow x=\pm 1 \vee x=\pm 3$$.
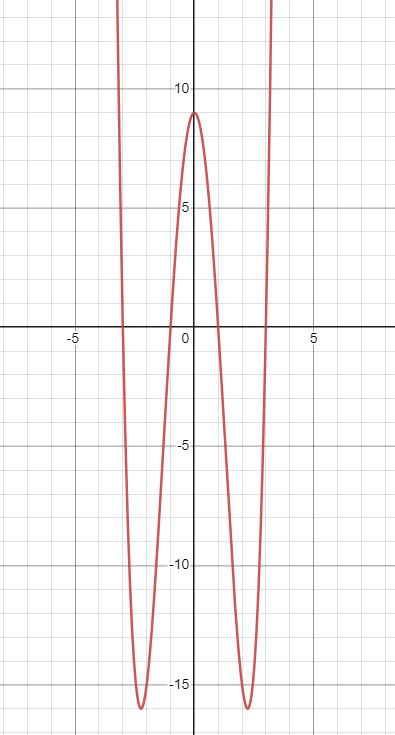
Zadanie 4.
$$p=\frac{2 ! 6 ! 6 !}{8 !}=\frac{3}{14}$$.
Zadanie 5.
$$x=\frac{\pi}{6}+2 k \pi$$ lub $$x=\frac{5}{6} \pi+2 k \pi, k \in Z$$

