ZBIORY - POJĘCIA WSTĘPNE
Zbiór jest jednym z pierwotnych pojęć matematycznych, a więc pojęciem nie definiowanym. Używane jest we wszystkich działach matematyki, podobnie jak w mowie potocznej, w znaczeniu kolekcji określonych obiektów np. zbiór uczniów w klasie, zbiór liczb pierwszych, zbiór rozwiązań nierówności itp.
Obiekty, które należą do danego zbioru nazywamy elementami tego zbioru.
Liczbę elementów zbioru nazywamy mocą zbioru.
Zbiory oznaczamy wielkimi literami, zaś ich elementy małymi.
Aby opisać zbiór, należy określić, jakie są jego elementy. Można to zrobić słownie lub (jeśli to możliwe) wypisując jego elementy, np.:
\(\mathbf{N}=\{0,1,2,3,4,5, \ldots\}-\) zbiór liczb naturalnych
Zbiór, który ma skończoną liczbę elementów, nazywamy zbiorem skończonym.
Zbiór, do którego należy nieskończenie wiele elementów, nazywamy zbiorem nieskończonym.
Aby zapisać, że element należy do zbioru, używamy symbolu \(\in\), np. \(5 \in \mathbf{N}\).
Aby zapisać, że element nie należy do zbioru - symbolu \(\notin\), np. \(\sqrt{3} \notin \mathbf{W}\).
Zbiór, do którego nie należy żaden element, nazywamy zbiorem pustym i oznaczamy symbolem \(\emptyset\).
Dwa zbiory \(A\) i \(B\) są równe, jeśli każdy element należący do zbioru \(A\) należy do zbioru \(B\) (czyli \(A \subset B\) ), a także każdy element w \(B\) należy do zbioru \(A\) (czyli \(B \subset A\) ). Tak więc:
\[
(A=B) \Longleftrightarrow(A \subset B \wedge B \subset A) .
\]
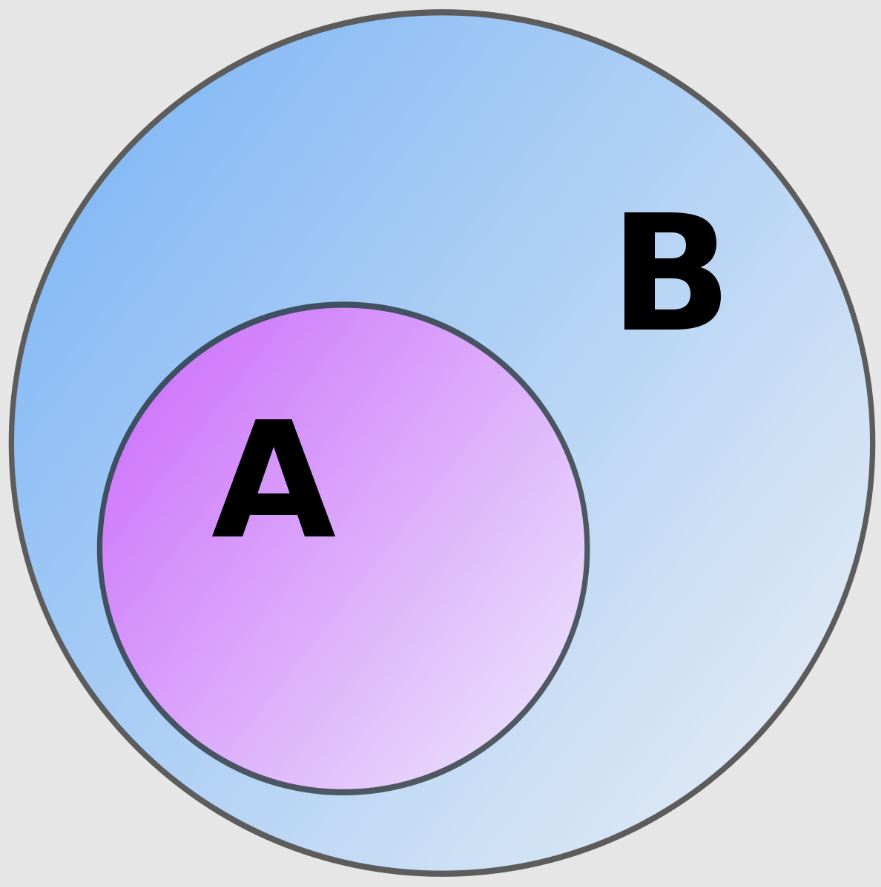
Zbiór \(A\) zawiera się w zbiorze \(B\), kiedy każdy element należący do zbioru \(A\) należy także do zbioru \(B\). Piszemy to w ten sposób: \(A \subset B\) lub \(A \subseteq B\). Zawieranie zbiorów nazywane jest także inkluzją. Zapis ten możemy czytać w różny sposób:
- ?Zbiór A zawiera się w zbiorze B"
- ?Zbiór A jest podzbiorem zbioru B?
- ?Zbiór B zawiera zbiór A?
Zbiór \(A\) jest podzbiorem zbioru \(B\), jeśli każdy element zbioru \(A\) jest elementem zbioru \(B\). Zapisujemy to: \(A \subset B\). Mówimy również, że zbiór \(A\) jest zawarty w zbiorze \(B\).
Zapis \(A \not \subset B\) oznacza, że \(A\) nie jest podzbiorem zbioru \(B\).
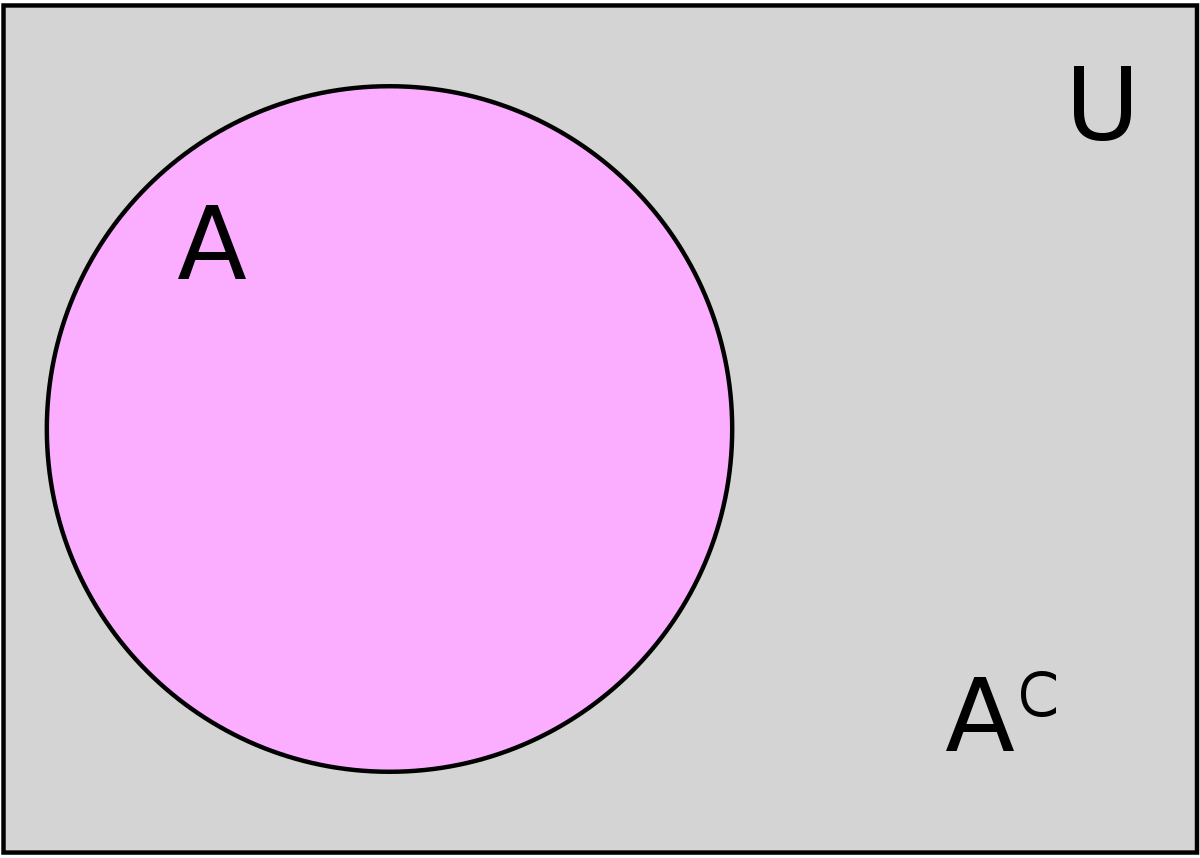
Dopełnieniem zbioru A z przestrzeni \(U\) nazywamy zbiór tych elementów przestrzeni \(U\), które nie należą do zbioru \(A\). Dopełnienie zbioru \(A\) oznaczamy jako \(A^{\prime}\) lub \(A^{c}\). Dopełnienie możemy zapisać tak: \(A^{\prime}=\{x: x \in U \wedge x \notin A\}\).
DZIAŁANIA NA ZBIORACH
Sumą zbiorów \(A\) i \(B\) nazywamy zbiór elementów, które należą do co najmniej jednego ze zbiorów: \(A\) lub \(B\). Sumę zbiorów \(A\) i \(B\) oznaczamy: \(A \cup B\).
\[
A \cup B=\{x: x \in A \text { lub } x \in B\}
\]
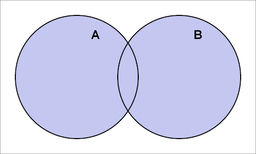
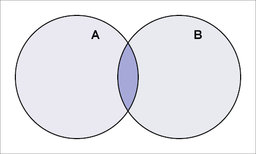
Iloczynem zbiorów \(A\) i \(B\) nazywamy zbiór elementów, które należą jednocześnie do obu tych zbiorów. Iloczyn zbiorów \(A\) i \(B\) oznaczamy: \(A \cap B\).
\[
A \cap B=\{x: x \in A \text { i } x \in B\}
\]
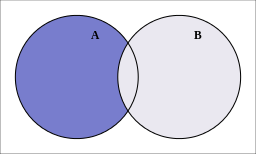
Różnicą zbiorów \(A\) i \(B\) nazywamy zbiór elementów, które należą do zbioru \(A\) i nie należą do zbioru \(B\). Różnicę zbiorów \(A\) i \(B\) oznaczamy: \(A \backslash B\) lub \(A - B\).
\[
A \backslash B=\{x: x \in A \text { i } x \notin B\}
\]
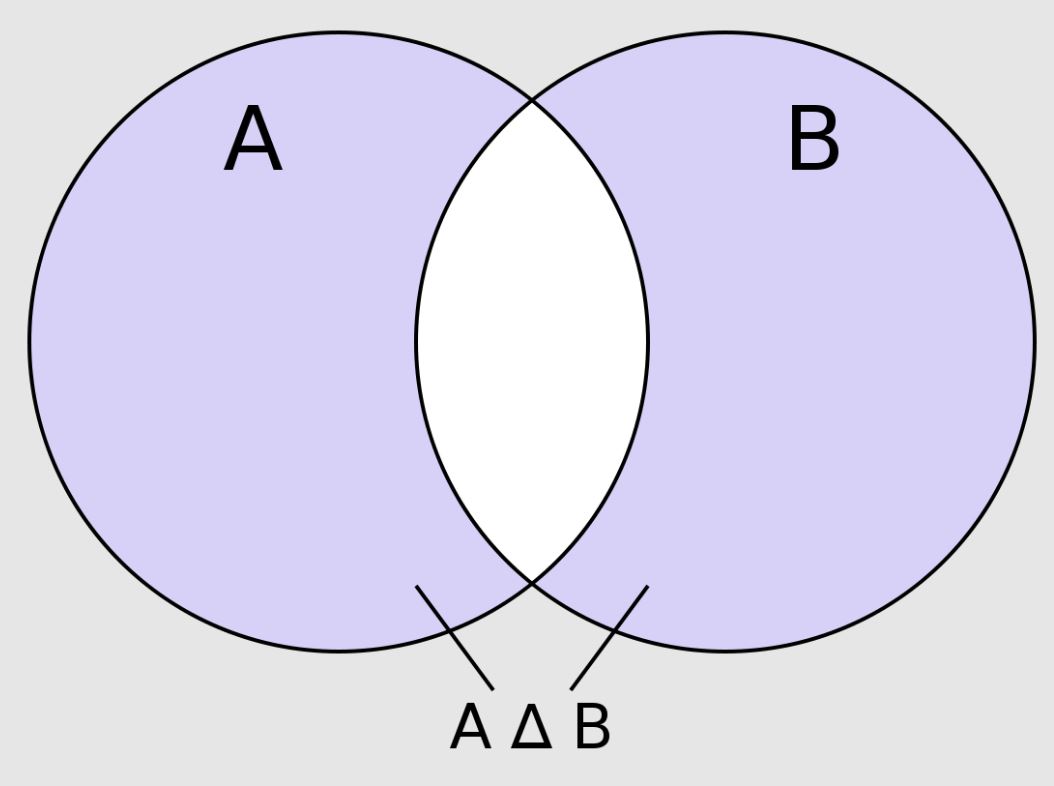
Różnicę symetryczną zbiorów \(A\) i \(B\) nazywamy zbiór składający się z elementów należących do dokładnie jednego ze zbiorów \(A\) i \(B\). Inaczej różnica symetryczna zbiorów \(A\) i \(B\), to zbiór elementów, które należą do zbioru \(A\) lub do zbioru \(B\), ale nie należą do obydwu naraz.
\[
\mathrm{A} \doteq \Delta B \Leftrightarrow\{x:(x \in A \wedge x \notin B) \vee(x \notin A \wedge x \in B)\}
\]
PRAWA DZIAŁAŃ NA ZBIORACH
\((A \cup B)^{\prime}=A^{\prime} \cap B^{\prime}\) - I prawo De Morgana
\((A \cap B)^{\prime}=A^{\prime} \cup B^{\prime}\) - II prawo De Morgana
\(A \cup B=B \cup A\) - przemienność dodawania zbiorów
\(A \cap B=B \cap A\) - przemienność mnożenia zbiorów
\((A \cup B) \cup C=A \cup(B \cup C)\) - łączność dodawania zbiorów
\((A \cap B) \cap C=A \cap(B \cap C)\) - łączność mnożenia zbiorów
\(A \cup(B \cap C)=(A \cup B) \cap(A \cup C)\) - rozdzielność dodawania zbiorów względem mnożenia
\(A \cap(B \cup C)=(A \cap B) \cup(A \cap C)\) - rozdzielność mnożenia zbiorów względem dodawania