Układy równań liniowych z dwiema niewiadomymi
Definicje, twierdzenia, interpretacja graficzna i cztery klasyczne metody rozwiązywania.
Definicja układu równań liniowych
Układem równań liniowych z dwiema niewiadomymi nazywamy układ, który da się przedstawić w postaci:
Nieformalnie: jest to „koniunkcja” dwóch równań, z których każde jest równaniem liniowym, tzn. obie niewiadome występują tylko w pierwszej potędze.
Wyznaczniki układu (metoda Cramera)
Wprowadzamy oznaczenia:
Wyznacznik główny układu:
\[ W = \left| \begin{array}{ll} a_1 & b_1 \\ a_2 & b_2 \end{array} \right| = a_1 b_2 - b_1 a_2 \]Wyznacznik po zmiennej \(x\):
\[ W_x = \left| \begin{array}{ll} c_1 & b_1 \\ c_2 & b_2 \end{array} \right| = c_1 b_2 - b_1 c_2 \]– zastąpiliśmy kolumnę z \(x\) kolumną z wyrazami wolnymi.
Wyznacznik po zmiennej \(y\):
\[ W_y = \left| \begin{array}{ll} a_1 & c_1 \\ a_2 & c_2 \end{array} \right| = a_1 c_2 - c_1 a_2 \]– tym razem kolumnę z \(y\) zastępujemy kolumną z wyrazami wolnymi.
Twierdzenie (metoda wyznaczników – przypadki)
Rozważamy układ
W zależności od wartości wyznaczników \(W, W_x, W_y\) mamy:
-
Jedno rozwiązanie, jeśli
\(W \neq 0\).
Wtedy układ ma dokładnie jedno rozwiązanie: \[ x = \frac{W_x}{W}, \quad y = \frac{W_y}{W}. \] -
Brak rozwiązań, jeśli
\(W = 0\)
oraz przynajmniej jeden z wyznaczników
\(W_x, W_y\) jest
różny od zera.
Oznacza to, że równania są sprzeczne (proste są równoległe, ale różne). -
Nieskończenie wiele rozwiązań, jeśli
\(W = W_x = W_y = 0\) i nie wszystkie współczynniki
\(a_1, b_1, a_2, b_2\) są równe zeru.
Wtedy oba równania opisują tę samą prostą (lub jedno jest jej wielokrotnością), a rozwiązaniem jest cała ta prosta.
Szczególna sytuacja pojawia się, gdy wszystkie współczynniki przy \(x\) i \(y\) znikają:
Jeżeli \(a_1 = b_1 = a_2 = b_2 = 0\), to układ przyjmuje postać
\[ \left\{ \begin{array}{l} 0 = c_1 \\ 0 = c_2 \end{array} \right. \]- jeśli dodatkowo \(c_1 = c_2 = 0\), to dowolna para \((x,y)\) jest rozwiązaniem (nieskończenie wiele rozwiązań w całej płaszczyźnie);
- jeśli co najmniej jedno z \(c_1, c_2\) jest różne od zera, układ jest sprzeczny (brak rozwiązań).
Interpretacja graficzna układu równań
Każde równanie liniowe z dwiema niewiadomymi można zapisać w postaci równania prostej w układzie współrzędnych. Układ dwóch równań reprezentuje więc dwie proste na płaszczyźnie.
Możliwe są trzy sytuacje:
- proste przecinają się w jednym punkcie → układ ma jedno rozwiązanie,
- proste pokrywają się → układ ma nieskończenie wiele rozwiązań,
- proste są równoległe i różne → układ nie ma rozwiązań.

Najczęściej stosowane metody rozwiązywania
W praktyce szkolnej korzystamy najczęściej z czterech metod:
Metoda podstawiania
Metoda podstawiania polega na tym, że z jednego z równań wyznaczamy jedną z niewiadomych, a następnie wstawiamy tak wyznaczone wyrażenie do drugiego równania. Po tym kroku otrzymujemy równanie z jedną niewiadomą.
Etapy:
- wyznacz z jednego równania \(x\) lub \(y\) (najlepiej tam, gdzie współczynnik jest prosty),
- podstaw to wyrażenie do drugiego równania,
- rozwiąż otrzymane równanie z jedną niewiadomą,
- podstaw otrzymaną wartość do wcześniejszego wyrażenia i wylicz drugą niewiadomą.
Rozwiąż układ równań:
\[ \left\{ \begin{array}{l} x + 2y = 7 \\ 3x - 5y = 3 \end{array} \right. \]Wyznaczamy z pierwszego równania \(x\):
\[ \left\{ \begin{array}{l} x = 7 - 2y \\ 3x - 5y = 3 \end{array} \right. \]Podstawiamy do drugiego równania:
\[ \left\{ \begin{array}{l} x = 7 - 2y \\ 3(7 - 2y) - 5y = 3 \end{array} \right. \] \[ \left\{ \begin{array}{l} x = 7 - 2y \\ 21 - 6y - 5y = 3 \end{array} \right. \Rightarrow \left\{ \begin{array}{l} x = 7 - 2y \\ -11y = -18 \end{array} \right. \] \[ \Rightarrow \left\{ \begin{array}{l} x = 7 - 2y \\ y = \dfrac{18}{11} \end{array} \right. \]Podstawiamy \(y\) do wzoru na \(x\):
\[ x = 7 - 2 \cdot \frac{18}{11} = \frac{77}{11} - \frac{36}{11} = \frac{41}{11}. \]Ostatecznie: \[ (x, y) = \left(\frac{41}{11}, \frac{18}{11}\right). \]
Metoda przeciwnych współczynników
Metoda przeciwnych współczynników polega na takim przekształceniu równań (mnożeniu przez odpowiednie liczby), aby przy jednej z niewiadomych pojawiły się współczynniki przeciwne. Wtedy dodajemy równania stronami i eliminujemy tę niewiadomą.
Etapy:
- wybierz niewiadomą, którą chcesz „usunąć”,
- pomnóż równania przez takie liczby, aby współczynniki przy tej niewiadomej były przeciwne,
- dodaj równania stronami, otrzymując równanie z jedną niewiadomą,
- rozwiąż je, a następnie podstaw do jednego z pierwotnych równań.
Rozwiąż układ równań:
\[ \left\{ \begin{array}{l} 3x + 2y = 12 \\ 5x - 7y = -11 \end{array} \right. \]Eliminujemy zmienną \(x\). Mnożymy:
\[ \left\{ \begin{array}{l} 3x + 2y = 12 \quad / \cdot 5 \\ 5x - 7y = -11 \quad / \cdot (-3) \end{array} \right. \] \[ \left\{ \begin{array}{l} 15x + 10y = 60 \\ -15x + 21y = 33 \end{array} \right. \]Dodajemy równania stronami:
\[ 15x + 10y - 15x + 21y = 60 + 33 \Rightarrow 31y = 93 \Rightarrow y = 3. \]Podstawiamy \(y=3\) do pierwszego równania:
\[ 3x + 2\cdot 3 = 12 \Rightarrow 3x = 6 \Rightarrow x = 2. \]Zatem rozwiązaniem układu jest para \((2,3)\).
Metoda wyznaczników (Cramera)
Metoda wyznaczników jest szczególnie przydatna przy dużych lub „brzydkich” liczbach (ułamki, duże współczynniki). Wymaga, aby układ był zapisany w postaci uporządkowanej:
Obliczamy wyznaczniki \(W, W_x, W_y\), a następnie korzystamy z twierdzenia o przypadkach (z sekcji powyżej).
Rozwiąż układ równań:
\[ \left\{ \begin{array}{l} 34x + 25y = 120 \\ 16x - 15y = 20 \end{array} \right. \]Obliczamy wyznaczniki:
\[ W = \left| \begin{array}{rr} 34 & 25 \\ 16 & -15 \end{array} \right| = 34\cdot(-15) - 25\cdot 16 = -510 - 400 = -910 \] \[ W_x = \left| \begin{array}{rr} 120 & 25 \\ 20 & -15 \end{array} \right| = 120\cdot(-15) - 25\cdot 20 = -1800 - 500 = -2300 \] \[ W_y = \left| \begin{array}{rr} 34 & 120 \\ 16 & 20 \end{array} \right| = 34\cdot 20 - 120\cdot 16 = 680 - 1920 = -1240 \]Ponieważ \(W \neq 0\), układ ma jedno rozwiązanie:
\[ x = \frac{W_x}{W} = \frac{-2300}{-910} = \frac{230}{91}, \quad y = \frac{W_y}{W} = \frac{-1240}{-910} = \frac{124}{91}. \]Ostatecznie: \[ (x, y) = \left(\frac{230}{91}, \frac{124}{91}\right). \]
Metoda graficzna
Metoda graficzna polega na narysowaniu w jednym układzie współrzędnych wykresów obu równań (prostych) i odczytaniu punktu ich przecięcia. W praktyce to metoda pomocnicza – wynik zależy od dokładności rysunku.
Rozwiąż graficznie układ równań:
\[ \left\{ \begin{array}{l} x + y = 4 \\ 3x - y = 8 \end{array} \right. \]Przekształcamy do postaci funkcji liniowych:
\[ \left\{ \begin{array}{l} y = 4 - x \\ y = 3x - 8 \end{array} \right. \]Rysujemy w jednym układzie współrzędnych wykresy funkcji \(f(x) = 4 - x\) oraz \(g(x) = 3x - 8\) i odczytujemy punkt ich przecięcia.
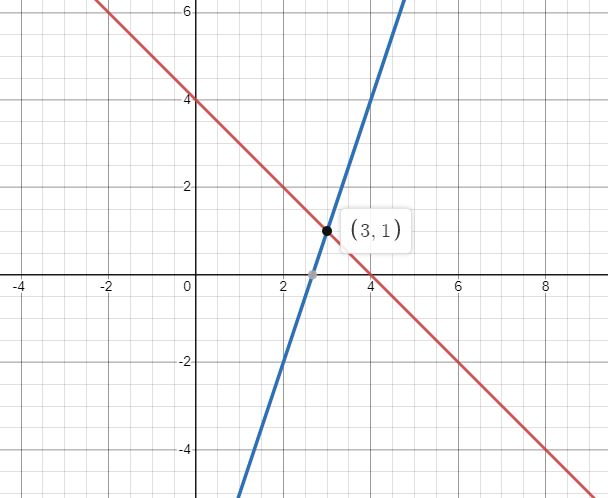
Odczytujemy z rysunku, że:
Lekcje wideo o układach równań liniowych
Chcesz zobaczyć metody rozwiązania „na żywo” na przykładach? Zobacz moje nagrania:

