Zadanie 1. [2021 Informator CKE, zad.3, 3 pkt]
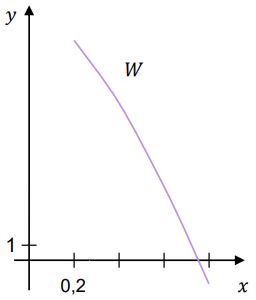
| Na diagramie obok przedstawiono fragment wykresu wielomianu $$W$$ określonego wzorem
$$W(x)=4 x^3-19 x^2-12 x+18$$ dla każdego $$x \in \mathbb{R}$$. Oblicz wszystkie pierwiastki wielomianu $$W$$. |
 |
Skorzystamy z twierdzenia o pierwiastkach wymiernych wielomianu o współczynnikach całkowitych.
Na mocy tego twierdzenia wnosimy, że jeśli wielomian $$W$$ ma pierwiastek wymierny, to należy on do zbioru
$$\mathbb{M}=\left\{\pm 1, \pm 2, \pm 3, \pm 6, \pm 9, \pm 18, \pm \frac{9}{2}, \pm \frac{9}{4}, \pm \frac{3}{2}, \pm \frac{3}{4}, \pm \frac{1}{2}, \pm \frac{1}{4}\right\}$$
Na podstawie fragmentu wykresu funkcji $$W$$ stwierdzamy, że jeden z pierwiastków wielomianu znajduje się w przedziale $$\left(\frac{3}{5}, \frac{4}{5}\right)$$. Tylko jedna liczba ze zbioru $$\mathbb{M}$$ leży w tym przedziale i jest to ułamek $$\frac{3}{4}$$.
Sprawdzamy, czy liczba $$\frac{3}{4}$$ jest pierwiastkiem wielomianu $$W$$ :
$$W\left(\frac{3}{4}\right)=4 \cdot\left(\frac{3}{4}\right)^3-19 \cdot\left(\frac{3}{4}\right)^2-12 \cdot \frac{3}{4}+18=\frac{27}{16}-\frac{171}{16}-\frac{144}{16}+\frac{288}{16}=0$$
Zatem wielomian jest podzielny przez dwumian $$\left(x-\frac{3}{4}\right)$$.
Dzielimy wielomian $$W$$ przez dwumian $$\left(x-\frac{3}{4}\right)$$ i zapisujemy go w postaci iloczynowej:
$$W(x)=\left(x-\frac{3}{4}\right)\left(4 x^2-16 x-24\right) .$$
Pierwiastkami trójmianu $$4 x^2-16 x-24$$ są liczby: $$2-\sqrt{10}$$ oraz $$2+\sqrt{10}$$.
Pierwiastkami wielomianu $$W$$ są liczby: $$2-\sqrt{10}, 2+\sqrt{10}$$ oraz $$\frac{3}{\pi}$$.
Zadanie 2. [2021 Informator CKE, zad.5, 3 pkt]
Wielomian $$W$$ jest określony wzorem $$W(x)=(x-1)\left(x^2-m x+m-1\right)$$ dla każdego $$x \in \mathbb{R}$$.
Wyznacz wszystkie wartości parametru $$m$$, dla których wielomian $$W$$ ma dokładnie jeden pierwiastek rzeczywisty.
Zauważmy, że liczba 1 jest pierwiastkiem wielomianu $$W$$. Zatem wielomian $$W$$ ma dokładnie jeden pierwiastek rzeczywisty tylko wtedy, gdy funkcja $$f(x)=x^2-m x+m-1$$ ma dokładnie jedno miejsce zerowe równe 1 lub gdy funkcja $$f$$ nie ma miejsc zerowych.
Zatem
$$\begin{gathered}\Delta<0 \text { lub }\left(\Delta=0 \text { i } x_0=1\right) \\m^2-4 m+4<0 \text { lub }\left(m^2-4 m+4=0 \text { i }-\frac{b}{2 a}=1\right) \\(m-2)^2<0 \quad \text { lub }\left((m-2)^2=0 \quad \text { i } \quad \frac{m}{2}=1\right)\end{gathered}$$
Nierówność $$(m-2)^2<0$$ jest sprzeczna, natomiast z warunków
$$(m-2)^2=0 \quad \text { і } \quad \frac{m}{2}=1$$
otrzymujemy $$m=2$$
Odp. $$m=2$$.
Zadanie 3. [2022 marzec, zad.4, 5 pkt]
Dane jest równanie
$$(x-6) \cdot\left[(m-2) x^2-4(m+3) x+m+1\right]=0$$
z niewiadomą $$x$$ i parametrem $$m \in \mathbb{R}$$.
Wyznacz wszystkie wartości parametru $$m$$, dla których to równanie ma trzy różne rozwiązania rzeczywiste tego samego znaku.
Zauważmy, że jednym z rozwiązań równania
$$(x-6) \cdot\left[(m-2) x^2-4(m+3) x+m+1\right]=0$$
jest liczba 6. Zatem równanie (1) ma trzy różne rozwiązania rzeczywiste tego samego znaku wedy i tylko wtedy, gdy równanie
$$(m-2) x^2-4(m+3) x+m+1=0$$
ma dokładnie dwa różne rozwiązania dodatnie $$x_1, x_2$$ takie, że $$x_1 \neq 6$$ i $$x_2 \neq 6$$.
Dla $$m=2$$ równanie (2) przyjmuje postać $$-20 x+3=0$$ i ma tylko jedno rozwiązanie.
Pozostaje wyznaczyć te wartości parametru $$m$$, dla których warunki zadania są spelnione, a równanie (2) jest kwadratowe, tj. wyznaczyć te wartości parametru, dla których spelnione są jednocześnie następujące warunki:
(W1) $$m-2 \neq 0$$
(W2) $$\Delta>0$$
(W3) $$x_1 \cdot x_2>0$$
(W4) $$x_1+x_2>0$$
(W5) $$(m-2) \cdot 6^2-4 \cdot(m+3) \cdot 6+m+1 \neq 0$$
Rozwiązaniem warunku (W1) jest $$m \neq 2$$.
Rozwiązujemy nierówność $$\Delta>0$$ :
$$\begin{gathered}{[-4(m+3)]^2-4 \cdot(m-2) \cdot(m+1)>0} \\16 m^2+96 m+144-4 m^2+4 m+8=0 \\12 m^2+100 m+152>0 \\m \in\left(-\infty,-\frac{19}{3}\right) \cup(-2,+\infty)\end{gathered}$$
Korzystając ze wzorów Viète'a, rozwiązujemy warunek (W3):
$$\begin{aligned}x_1 \cdot x_2 &>0 \\\frac{m+1}{m-2} &>0 \\(m+1)(m-2) &>0 \wedge m \neq 2 \\m \in(-\infty,-1) & \cup(2,+\infty)\end{aligned}$$
Korzystając ze wzorów Viète'a, rozwiązujemy warunek (W4):
$$x_1+x_2>0$$
$$\begin{gathered}-\frac{-4(m+3)}{m-2}>0 \\(m+3)(m-2)>0 \wedge m \neq 2 \\m \in(-\infty,-3)\cup(2,+\infty)\end{gathered}$$
Rozwiązujemy warunek (W5):
$$\begin{gathered}(m-2) \cdot 6^2-4 \cdot(m+3) \cdot 6+m+1 \neq 0 \\13 m-143 \neq 0 \\m \neq 11\end{gathered}$$
Wyznaczamy część wspólną rozwiązań warunków (W1)-(W5) i otrzymujemy $$m \in\left(-\infty,-\frac{19}{3}\right) \cup(2,11) \cup(11,+\infty)$$
Równanie (1) ma trzy różne rozwiązania tego samego znaku dla $$m \in\left(-\infty,-\frac{19}{3}\right) \cup(2,11) \cup(11,+\infty)$$

